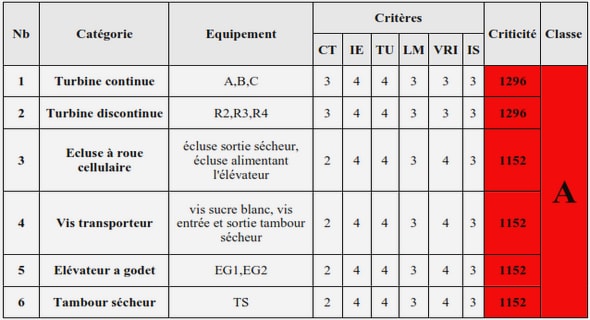
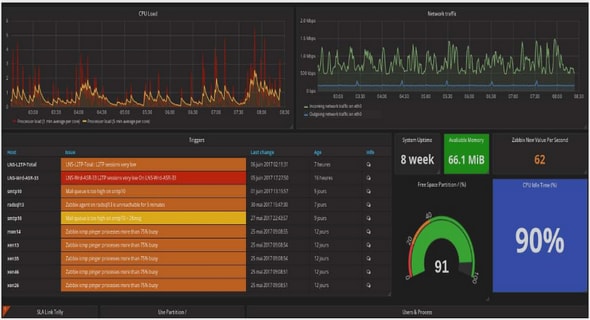
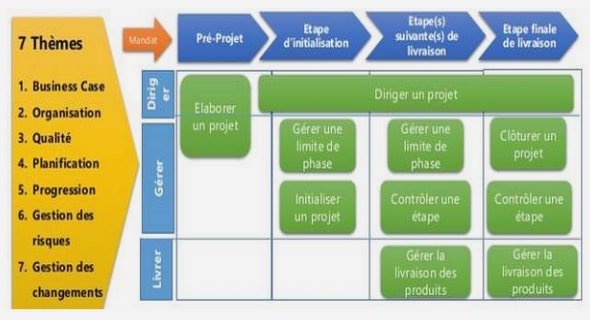
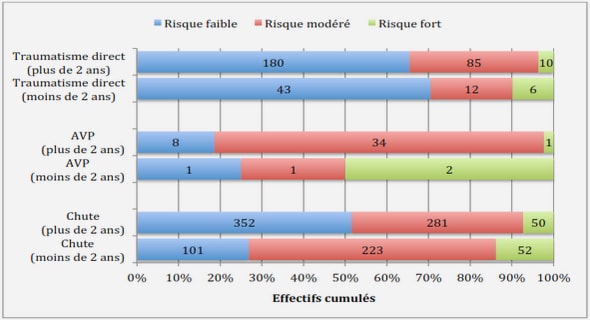
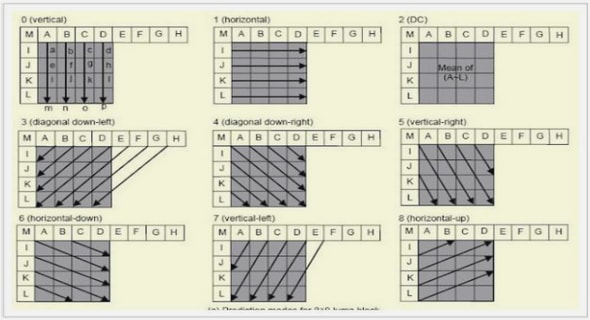
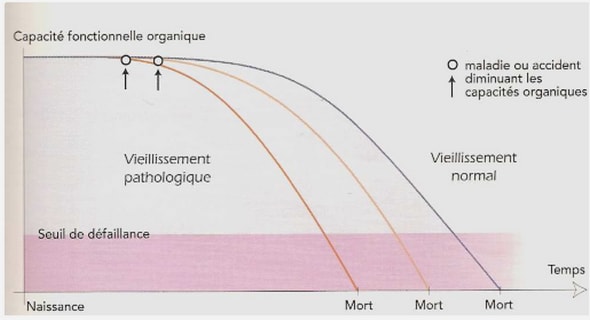
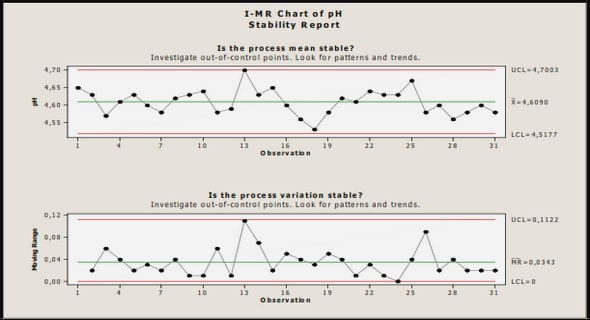
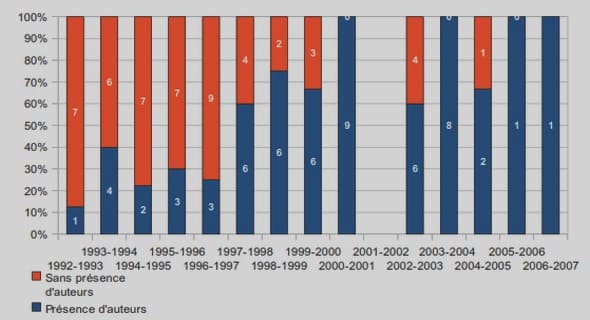
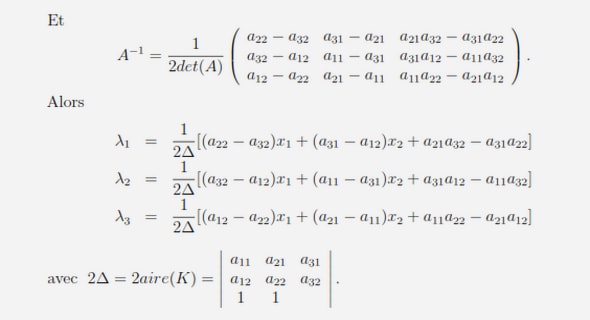Utilisation des MCMC Conclusion et discussion Les méthodes de Monte-Carlo présentées dans ce document permettent de…
Mathématiques
PFE mathématiques : voici quelques idées de projets de fin d’études en mathématiques :
Optimisation et algorithmes
- Application à des problèmes réels comme la logistique, les réseaux de transport, ou la finance.
Analyse des données et statistiques
- Application des méthodes statistiques pour l’analyse des données massives (big data).
Mathématiques financières
- Étude des produits dérivés et des modèles de valorisation d’options (ex. : modèle de Black-Scholes).
Théorie des graphes et réseaux
- Étude des algorithmes de parcours, de connectivité, et d’optimisation des réseaux.
Équations différentielles et systèmes dynamiques
- Application aux phénomènes physiques, biologiques, ou économiques.
Cryptographie et sécurité informatique
- Analyse de la sécurité des systèmes de communication et des transactions en ligne.
Mathématiques et intelligence artificielle
- Étude des algorithmes d’apprentissage supervisé et non supervisé.
Géométrie et topologie
- Application à la modélisation des formes et des structures en biologie et en physique.
Mathématiques appliquées à l’ingénierie
- Utilisation des méthodes numériques pour la résolution des équations aux dérivées partielles.
Théorie des nombres et ses applications
- PFE mathématiques applications en cryptographie, en théorie des codes, et en informatique.
Analyse fonctionnelle et applications
- Application à la mécanique quantique et à la théorie des opérateurs.
Méthodes probabilistes et processus stochastiques
- Modélisation des processus aléatoires et des systèmes probabilistes.
Contribution à la modélisation et à la commande assistive basée, intention d’un exosquelette du membre inférieur
Système neuro-musculaire et organisation neurologique du mouvement Les muscles striés squelettiques assurent, sous le contrôle du…
Traditions et réformes de l’enseignement des mathématiques à l’époque des mathématiques modernes
LE MOUVEMENT DES « MATHEMATIQUES MODERNES » A L’ECHELLE INTERNATIONALE Les débuts de la coopération internationale…
Hypothèses minimales de synchronie pour le consensus byzantin avec signatures
État de l’art Le problème du consensus et les comportements byzantins ont été introduits par Lamport,…
Risque de crédit: modélisation et simulation numérique
Sur le premier temps de défaut et après Le premier chapitre commence par une revue…
Variétés approximativement Kähleriennes et variétés de Gray
G-structures et réductions des G-structures Soit M une variété réelle de dimension m, TM son…
Diffraction Inverse par des Inclusions Minces et des Fissures
Imaging of Thin Penetrable Inclusions by a MUSICType Algorithm The imaging of a thin inclusion,…
Systèmes locaux rigides et transformation de Fourier
MODULES SUR LES ANNEAUX D’OPÉRATEURS DIFFÉRENTIELS Le but de ce chapitre introductif est de rappeler,…
Systèmes locaux rigides et transformation de Fourier
MODULES SUR LES ANNEAUX D’OPÉRATEURS DIFFÉRENTIELS Le but de ce chapitre introductif est de rappeler,…
Crises de liquidité endogènes dans les marchés financiers
Market participants A market is a place where buyers meet sellers to execute transactions. The…
Autour de l’algorithme du Langevin extensions et applications
Some preliminaries on Markov chains Markov chains are a class of stochastic processes commonly used…
Cycles proches, cycles évanescents et théorie de Hodge pour les morphismes sans pente
Hodge theory In [Ste76] J. H. M. Steenbrink constructed a mixed Hodge structure on the…
Limite Hydrodynamique pour un Gaz Sur Réseau de Particules Actives
Modèle de Vicsek et transition de phase dans les dynamiques d’alignement Les phénomènes d’auto-organisation…
Stabilité des solitons et des multi-solitons pour l’équation de Landau-Lifshitz
Cas des sommes de solitons On se place dans une situation plus compliquée qu’un seul…
Modélisation mathématique de la malaria leishmanioses
Modélisation mathématique de la malaria leishmanioses Dynamique de population Introduction général L’espèce humaine constitue l’une des…
Mathématiques Floues
Mathématiques Floues La theorie des ensembles floues Définition d’un sous ensemble flou Dans la théorie des…
Reconstruction des Images 2-D à partir des Moments Discrets
Reconstruction des Images 2-D à partir des Moments Discrets Le Moment de Hahn Les polynômes de…
Surface de Riemann
Surface de Riemann Fonctions holomorphes méromorphes sur des surface de Riemann Dans cette partie on vas…
Application sur les suites monotones
Application sur les suites monotones La théorie de Ramsey infini Le théorème de ramsey infini Un…
Stabilité et bornitude des solutionsd’une classe d’équations différentielles vectorielles du troisième ordre avec retard
Stabilité et bornitude des solutionsd’une classe d’équations différentielles vectorielles du troisième ordre avec retard INTRODUCTION La…
Information dans les jeux
Information dans les jeux Pas d’équilibre,trop d’équilibre Il est important de noter que tous les jeux…
Jeux à somme nulle en stratégies mixtes
Jeux à somme nulle en stratégies mixtes Jeux à somme nulle en stratégies pures Modèle Formellement,…
La théorie des ensembles flous
La théorie des ensembles flous Opérations sur les sous-ensembles flous Proposition 2.3.1. On définit en théorie…
La méthode du maximum de vraisemblance
La méthode du maximum de vraisemblance Contribution principale L’objectif principal de ce chapitre est d’étudier le…
Transformée de Darboux en une dimension
Transformée de Darboux en une dimension Introduction Qu’arrive-t-illorsque l’on décide de modifier la décomposition habituelle en…
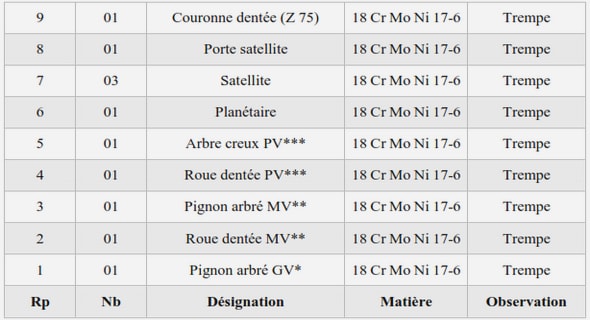
La gestion des tolérances
La gestion des tolérances Tolérance de position – Tolérance de localisation La tolérance de position (ou…
Généralités et rappels sur les processus stochastiques
Description et décomposition d’une série chronologique 9 GÉNÉRALITÉS ET RAPPELS SUR LES PROCESSUS STOCHASTIQUES Avant de…
Réseaux de neurones articiels et apprentissage
Réseaux de neurones articiels et apprentissage RÉSEAUX DE NEURONES ARTIFICIELS ET APPRENTISSAGE Introduction La mise au…
Calculs de précision dans un modèle supersymétrique non minimal
Il aura fallu plus d’un siècle, de la découverte de l’électron par Thomson en 1897 à…
Constante systolique et variétés plates
La structure des variétés plates Une variété riemannienne plate est une variété riemannienne localement isométrique…