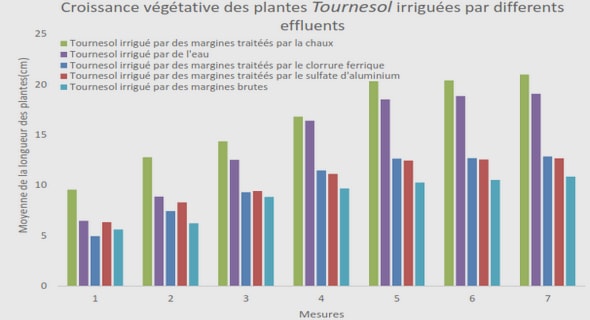
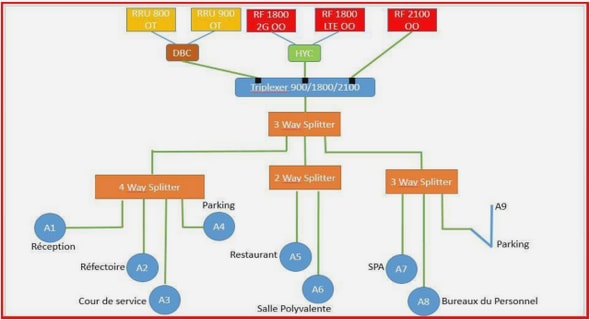
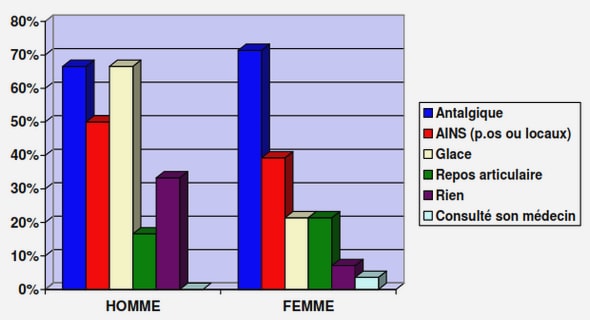
Télécharger le fichier pdf d’un mémoire de fin d’études
Caractéristique de l’erreur d’observation de l’observateur
Le filtre de paramètre
θ (j0) ,θ (j1) ,…,θ (ji) ,…,θ (jq)
Les bornes du ième intervalle sont θ (ji−1) et θ (ji) .
Construction du filtre de paramètre
• d’un observateur d’isolation ( xˆ(ij ) )
• deux modèles de seuil qui produisent deux états des seuils, ( xa (ij ) , xb (ij ) )
• deux observateurs d’états des seuils qui produisent deux seuils dynamiques ( xˆa (ij ) , xˆb (ij ) )
Pour ces deux raisons, les domaines des paramètres devraient être divisés en plus petits intervalles. Ceci implique une augmentation du nombre de filtres de paramètres et par conséquent un temps de calcul plus important. Pour pallier ces problèmes, nous proposons dans ce chapitre une nouvelle version basée sur l’utilisation des seuils adaptatifs.
Après l’occurrence d’un défaut, dans chaque filtre de paramètre, on fait fonctionner l’observateur d’isolation comme un observateur adaptatif qui identifie en ligne le paramètre du système. En même temps, on fait fonctionner les deux observateurs d’états des seuils en tant qu’observateurs adaptatifs qui identifient en ligne les paramètres des deux modèles de seuil. Soit au total trois observateurs adaptatifs qui ont un même gain d’identification. Le choix de ces gains doit garantir que les procédures d’identification soient sans dépassement (monotone en fonction du temps). Dans ce chapitre, l’observateur d’isolation, les observateurs des seuils et les seuils employés dans le chapitre 2 sont les mêmes sauf qu’ils sont adaptatifs. Toutes les notations et les hypothèses faites dans le chapitre précédent sont les mêmes sauf dans quelques cas particuliers que nous mentionnerons.
Dans ce chapitre, en éliminant les seuils, nous proposons une nouvelle version de la méthode proposée dans les chapitres précédents dans laquelle nous n’avons besoin que de ( q +1) observateurs pour q intervalles [49]. Avec cette nouvelle version, nous avons les mêmes performances d’isolation et d’identification de défaut comme celle proposée dans les chapitres précédents. Dans ce chapitre, les structures du système non linéaire et de l’observateur sont les mêmes que celles présentées dans les chapitres précédents. Seules les notations concernant les intervalles vont changer.
On suppose qu’avant t f , l’état xˆ(t) de l’observateur a convergé vers l’état x(t) du système, ainsi e(t f ) = 0 et ε (t f ) = 0 .
|
Table des matières
Introduction
Chapitre 1 -Observateurs non linéaires et détection de défauts
1.1 Formulations des systèmes dynamiques non linéaires de défaut
1.2 Caractéristique distinguable de l’espace de paramètre
1.3 Observateur non linéaire et observateur adaptatif non linéaire
1.3.1 Observabilité
1.3.2 Observateur
1.3.3 Observateur adaptif non linéaire
1.4 Détection de défauts
Chapitre 2 -Isolation et identification de défauts avec des seuils non adaptatifs
2.1 Le principe de la méthode
2.2 Caractéristique de l’erreur d’observation de l’observateur
2.3 Le filtre de paramètre
2.3.1 Construction du filtre de paramètre
2.3.2 Principe du filtre de paramètre
2.4 Mécanisme d’isolation du défaut
2.4.1 Filtre de défaut
2.4.2 Isolation de défaut
2.5 Caractéristiques de la méthode
2.5.1 Vitesse d’isolation de la méthode
2.5.2 Identification du paramètre défectueux
2.5.3 Condition d’isolation
2.5.4 Partition du domaine du paramètre
2.6 Simulation
2.6.1 Modèle du procédé
2.6.2 Filtre de paramètre
2.6.3 Illustration de la propriété de monotonicité
2.6.4 Isolation de défaut
2.7 Conclusion
Chapitre 3 -Isolation et identification de défauts avec des seuils adaptatifs
3.1 Filtre adaptatif de paramètre
3.2 Principe du filtre adaptatif de paramètre
3.3 Isolation de défaut
3.4 Estimation des paramètres
3.5 Seuils des procédures d’identification des paramètres
3.5.1 Le cas où l’égalité c ob(ij) = c oba(ij) = c obb(ij) = c (ij) n’est pas satisfaite
3.5.2 Le cas où les dynamiques des trois observateurs sont différentes
3.6 Simulation
3.6.1 Le filtre de défaut
3.6.2 Simulation pour l’isolation de défaut et l’identification de défaut
3.7 Conclusion
Chapitre 4 -Isolation et identification de défauts sans seuils
4.1 Filtre de paramètre
4.1.1 Etude préliminaire
4.1.2 Formulation du filtre
4.2 Principe de l’isolation et de l’identification de défaut
4.2.1 filtre de défaut
4.2.2 Isolation et identification de défaut
4.2.3 Vitesse d’isolation
4.3 Version adaptative
4.4 Simulation
4.4.1 Le filtre de défaut
4.4.2 Simulation pour l’isolation de défaut et l’identification de défaut
4.4.3 Simulation pour l’influence des gains d’identification
4.5 Conclusion
Conclusion
Références
Télécharger le rapport complet