Outils ab initio de la chimie quantique

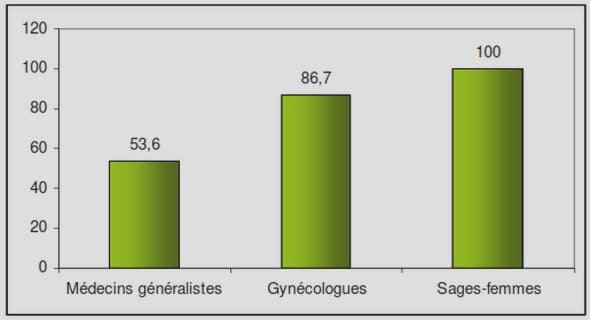
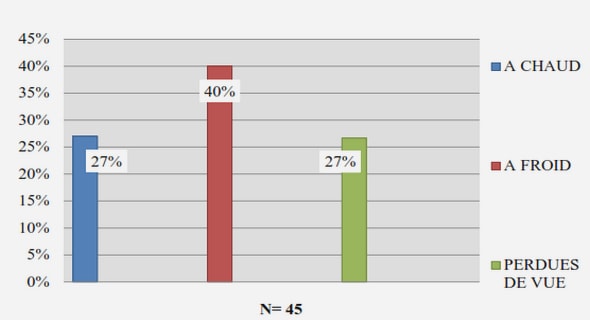
L’apparition de la vie sur la Terre et celle de nouveaux éléments chimiques dans l’univers ont fait l’objet de plusieurs études portant sur les différentes réactions et interactions survenant au sein des galaxies et des étoiles. Parmi ces études on peut citer celle sur la dynamique stellaire, la formation des galaxies, les structures matérielles à grande échelle de l’univers, l’origine des rayons cosmiques, la relativité générale et la physique des particules. Dans ce travail nous sommes intéressés à l’étude de la dynamique moléculaire de systèmes à N corps par des méthodes analytiques qui nécessite l’utilisation de calculs numériques pour l’obtention de données qui étaient auparavant difficile à calculer pour certains de ces systèmes. Les éléments chimiques auxquels nous nous intéressons se trouvent dans le milieu interstellaire(MIS) où l’observation par télescopie dans le domaine de l’infrarouge a permis la découverte de plusieurs nouvelles molécules. Le milieu interstellaire est la matière qui, dans une galaxie, remplit l’espace entre les étoiles renfermant une grande quantité de gaz(Hydrogène surtout et Hélium ), de la poussière interstellaire et de rayons cosmiques. En effet le MIS est composé de rayons cosmiques, de grains de poussière, d’atomes comme 1H, 12C, 16O et 14N et de molécules telles que CN, CN­, HCN, CO, OH, CS, H2CO, … et du fait des réactions thermonucléaires, il s’enrichit de plus en plus. Ainsi on assiste dans ce MIS à une forte abondance de molécules comportant le groupement ­CN (cyano). De nos jours, plusieurs observations(Petrie, Millar & Markwick (2003) et Kołos & Grabowski (2000)) ont montré l’abondance des dicyanopolyynes( N C–(C C)n –C N). La mol ≡ ≡ ≡ écule isocyanogéne CNCN qui fait l’objet de notre étude a été trouvée dans le milieu interstellaire plus précisément dans les nuages denses L483 dans le TMC­1 en observant diverses transitions de rotation dans la bande de 3mm avec le télescope IRAM ( l’Institut de Radioastronomie Millimétrique) de 30m. Des études expérimentales (Vastel et al. (2019)) ont montré les raies d’émission de CNCN détectées avec les transitions (10­9, 9­8, 8­7 et 7­6). Sa forme protonée NCCNH+ a également été observé vers les nuages sombres et froids TMC­1 et L483 à 44 GHZ par le téléobjectif Yebes 40 m et à 88,8 GHz par le télescope IRAM de 30 m, respectivement (Agúndez et al. (2015)).

Outils ab initio de la chimie quantique

Équation de Schrödinger du système polyélectronique

L’équation différentielle de Schrödinger étant linéaire dans le cas de l’atome d’hydrogène ou l’ion hydrogénoïde ne l’est plus dans le cas de l’atome polyélectronique (en raison des répulsions électroniques). Le comportement de ce système moléculaire peut être décrit par l’équation de Schrödinger indépendant du temps suivante:

H Ψ (Rα,ri)=E Ψ (Rα,ri) (1.1)

où Ψ(Rα, ri) est la fonction d’onde du système avec Rα la coordonnée radiale des noyaux et ri est celle des électrons.
Ĥ est l’hamiltonien du système.
Les indices α et i représentent respectivement le noyau et l’électron .
E est l’énergie du système .

Hamiltonien du système polyélectronique

L’hamiltonien non relativiste du système polyélectronique isolé, en l’absence de champ externe, s’écrit comme la somme de plusieurs opérateurs ci­dessous:

H=Tn+Te+V ee+Ven+Vnn (1.2)

L’approximation du Born-Oppenheimer

L’utilisation de cette approximation consiste en la séparation de la partie électronique et la partie nucléaire de l’hamiltonien du système considéré. Sachant que la masse des électrons est 2000 fois plus faible que celle des protons, la vitesse des électrons est plus grande que celle des noyaux, c’est la raison pour laquelle on néglige l’opérateur cinétique des noyaux et par conséquent l’opérateur de répulsion entre noyau­noyau devient constante du fait que le noyau est immobile par rapport aux électrons. Ainsi l’hamiltonien électronique He s’écrit:

He =T e+Vee+V en+V nn

et l’hamiltonien nucléaire est Hn=Tn

La fonction d’onde totale du système est le produit de fonctions d’onde électronique et nucléaire:

Ψ (Rα, ri)=Ψ (ri, Rα)Ψ (Rα) (1.4)

Ψ( ri, Rα) est la fonction d’onde électronique qui dépend des coordonnées des électrons et paramétriquement celles des noyaux.
Ψ ( Rα ) est la fonction d’onde des noyaux qui dépend des coordonnées des noyaux.

La méthode de Hartree­Fock (HF)

L’approximation des électrons indépendants

En considérant la partie électronique, l’opérateur de répulsion électron­électron rend difficile la résolution de l’équation de Schrödinger électronique. Pour surmonter cette difficulté on fait appel à l’approximation des électrons indépendants qui vise à négliger cette partie. Dans cette approximation le principe de l’indiscernabilité dit qu’on ne peut pas identifier le cas ou le système est décrit par la fonction Ψ(r1 ,r2,…,ri,…,rj,…,rN ) ou par Ψ (r1 ,r2,…,rj,…,ri,…,rN ) en permutant les deux indices i et j. Ces deux fonctions décrivent le même état physique. L’opérateur de permutation Pij agissant sur la fonction d’onde donne: Pij Ψ (r1,r2,… ,ri,…,rj,…,rN)=−Ψ (r1,r2,… ,ri,… ,rj,…,rN) (1.7)

Pij²Ψ (r1, r2,… ,ri,…,rj,…, rN)=a2Ψ (r1,r2,… , ri,…,rj, …,rN) (1.8)

Avec Pij² =1 , d’où a=±1

Dans cette approximation, chaque électron se trouvant dans un état stationnaire, est affecté par le champ des autres électrons et des noyaux.

Le principe variationnel

Dans la m éthode ab initio, l’application du principe variationnel sur les fonctions d’ondes d’essai, donne des énergies qui ne peuvent jamais être inférieures à l’énergie exacte. Dans ce cas, on peut toujours améliorer la convergence de l’énergie en améliorant simultanément les fonctions d’ondes. La base principale de la méthode de Hartree­Fock est le principe variationnel. Il permet de déterminer l’orbitale et l’énergie d’un atome ou d’une molécule. Dans ce principe pour une fonction approchée du système, l’hamiltonien de l’état fondamental dépend d’un paramètre ajustable µ et l’énergie moyenne E(µ)=<Ψ |H|Ψ > est toujours supérieure à l’énergie fondamentale E0. Ce principe appliqué donc à la fonction d’onde d’essai donne toujours des énergies qui sont supérieures ou égales à l’énergie exacte.

Table des matières

Introduction Générale
Chapitre I:Outils ab initio de la chimie quantique
I-Outils ab initio de la chimie quantique
I.1- Introduction
I.2-Équation de Schrödinger du système polyélectronique
I.3-Hamiltonien du système polyélectronique
I.4-L’approximation du Born-Oppenheimer
I.5-La méthode de Hartree-Fock (HF)
I.5.1-L’approximation des électrons indépendants
I.5.2-Le principe variationnel
I.5.3-Déterminant de Stater
I.5.4-La méthode de Hartree-Fock
I.6-La méthode de Clusters couplés(CC)
I.7-Conclusion
Chapitre II:THÉORIE DE COLLISION
II- THÉORIE DE COLLISION
II.1-Excitation rotationnelle de molécules linéaires par collision avec les atomes
II.1.1-L’approche du couplage fermé (Close Coupling CC)
II.1.1.1-La fonction d’onde
II.1.1.2-Équations couplées
II.1.1.3-Sections efficaces de transition rotationnelle
II.1.2-Les méthodes d’approximations
II.1.2.1-L’approximation des états couplés (Coupled States CS)
II.1.2.2-L’approximation soudaine d’ordre infinie (Infinite Order Sudden IOS)
II.1.3-Taux de collisions
II.2-Calculs dynamiques
II.2.1-Paramètres de calcul
Chapitre III:RÉSULTATS ET DISCUSSIONS
III- RÉSULTATS ET DISCUSSIONS
III.1-Surface d’énergie potentiel (SEP)
III.2-Section efficace
III.2-1-Section efficace
III.2-1-Section efficace
III.3-Taux de collision
CONCLUSION ET PERSPECTIVE
ANNEXE

Lire le rapport complet