Langage mathématique, discours mathématique, expressions mathématiques

Télécharger le fichier pdf d’un mémoire de fin d’études

Logique des mathématiques et logique mathématique

Dans cette recherche, je considère la logique et les mathématiques comme deux domaines dont l’intersection non vide délimite un champ que j’appellerai la logique des mathéma-tiques et que je propose de définir ainsi :

Ensemble des moyens, des procédés selon lesquels sont organisés le discours et le raisonnement en mathématiques, vus sous un double aspect de correc-tion syntaxique d’une part (vérifier que les règles d’usage de la langue sont respectées) et de validité sémantique d’autre part (pouvoir s’assurer que les raisonnements aboutissent à des vérités).

La logique des mathématiques est ce que j’ai déjà appelé dans l’introduction la logique à l’œuvre dans l’activité mathématique. La manière de rendre compte de cette logique des mathématiques, en lui fournissant notamment un vocabulaire et des notations, a beaucoup évolué. La logique mathématique peut alors être vue comme une approche récente et, en utilisant une terminologie moderne, on pourra dire que la logique mathématique est une modélisation de la logique des mathématiques, au sens de la construction d’un modèle mathématique qui rend compte d’une réalité existante. C’est ce qu’expliquent R. Cori et D. Lascar dans l’introduction de leur manuel Logique mathématique :

[Le mathématicien cherche] à donner une représentation mathématique d’une situation (plus ou moins) « concrète », à répondre à un besoin exprimé l’extérieur du monde mathématique, en fournissant un outil mathématique eﬃcace (les espaces vectoriels, représentant, au départ, l’espace physique dans lequel nous vivons, sont l’illustration la plus banale de ce propos). La logique, elle, suit le même processus ; sa particularité est qu’elle tente de décrire, non une réalité extérieure au monde mathématique, mais cette réalité que sont les mathématiques.

Cela ne doit pas être gênant, à condition que l’on sache précisément de quoi il va s’agir. Aucun étudiant ne fait de confusion entre son environnement physique et un espace vectoriel orienté de dimension 3, mais la connaissance de cet environnement aide à avoir une bonne intuition lorsqu’il faut démontrer une propriété de la structure mathématique en question. En logique, c’est la même chose : nous allons en quelque sorte faire une copie, une maquette, osons dire un modèle réduit, de l’univers mathématique qui nous est (relativement) familier. (Cori & Lascar, 1993, pp. 4-5)

Un enseignement de logique au service de l’activité mathématique aurait ainsi pour but d’enseigner cette logique des mathématiques, c’est-à-dire cet ensemble de connaissances sur la façon de s’exprimer et de raisonner en mathématiques.

Étudier la transposition didactique de notions de logique au lycée

Une question de recherche en didactique relative à cet enseignement aurait alors pu être :

Un changement dans les programmes de mathématiques pour le lycée est venu modifier le contexte institutionnel d’un tel enseignement et a influencé mon approche didactique. En eﬀet, dans le nouveau programme pour la classe de Seconde publié en juillet 2009 (et dans ceux qui ont suivi en 2010 pour la classe de Première et en 2011 pour la classe de Terminale), des notions de logique sont explicitement citées (les connecteurs ET et OU, les quantificateurs universels et existentiels, les propositions conditionnelles, la négation, les types de raisonnement 1), ce qui n’était pas le cas dans les programmes qui précédaient, et des objectifs y sont associés. Les professeurs de lycée ont ainsi actuellement à enseigner des notions de logique. Il y a une demande institutionnelle et ma recherche porte sur la mise en œuvre de cette demande.

Les mathématiciens partagent certains savoirs sur des notions de logique, nécessaires pour leur activité. Je suivrai dans cette thèse la démarche de la Théorie Anthropologique du Didactique en étudiant les nécessaires transformations de ces savoirs en vue de les enseigner, c’est-à-dire le processus de transposition didactique de ces notions au lycée, tel que défini par Y. Chevallard dans La transposition didactique :

Un contenu de savoir ayant été désigné comme savoir à enseigner subit dès lors un ensemble de transformations adaptatives qui vont le rendre apte à prendre place parmi les objets d’enseignement. Le « travail » qui, d’un objet de savoir à enseigner, fait un objet d’enseignement est appelé la transposition didactique. (Chevallard, 1991, p. 39)

Ce processus de transposition didactique se fait en deux étapes :

– la transposition didactique externe, du savoir savant au savoir à enseigner ;

– la transposition didactique interne, du savoir à enseigner au savoir enseigné.

Dans cette thèse, je m’intéresse principalement à la première étape de la transposition didactique. Je cherche en eﬀet à montrer, et à expliquer, la complexité du savoir à ensei-gner.

Savoir savant, savoir de référence, première question de recherche

Dans La transposition didactique en mathématiques, G. Arsac distingue des objets d’en-seignement « qui sont introduits explicitement par une définition, suivie de la liste de leurs propriétés » et des objectifs d’enseignement « du type : savoir raisonner, savoir ar-gumenter (ce qui concerne d’autres disciplines que les mathématiques), savoir résoudre les problèmes » (Arsac, 1989, p. 17). La logique des mathématiques serait plutôt du côté des objectifs d’enseignement, mais en listant des notions de logique et en y associant des savoirs (même si ce sont plutôt des savoir-faire), les nouveaux programmes pour le lycée amorcent un déplacement de ces notions de logique vers des objets d’enseignement. Ils réservent cependant à ces notions un traitement diﬀérent d’autres notions au programme. Par exemple, la notion d’échantillon 2 est un « contenu » 3 du programme, associé à des capacités attendues » – comme « exploiter et faire une analyse critique d’un résul-tat d’échantillonnage » – et accompagné du « commentaire » suivant : « un échantillon de taille est constitué des résultats de répétitions indépendantes de la même expé-rience. » Les notions de logique par contre ne sont pas présentées comme des contenus et ne sont pas accompagnées d’un commentaire qui en donnerait ce qui pourrait être une définition au niveau du lycée. La notion d’échantillon est clairement repérée dans un sa-voir savant (la statistique), dont les concepteurs de programmes se saisissent et font un objet d’enseignement. Pour les notions de logique, ce statut ambivalent entre objectifs et objets d’enseignement m’amène à envisager diﬀéremment le processus de transposition didactique.

Nous avons vu que ce qui était visé était l’acquisition de la logique des mathématiques et non de connaissances en logique mathématique, que ce qui était partagé par la com-munauté mathématique était plutôt de l’ordre des « savoirs en acte » que d’un savoir décontextualisé, dépersonnalisé, formalisé. La logique des mathématique est visible dans les pratiques des mathématiciens plutôt que dans des traités. J’emprunte alors à J. Ro-galski et R. Samurçay la notion de savoir de référence, qu’elles utilisent dans Modélisation d’un « savoir de référence » et transposition didactique dans la formation de professionnels de haut niveau :

Dans le domaine étudié, on assiste au déroulement d’un processus de construction d’un corps de savoir de référence à partir d’un ensemble de « sa-voirs en acte » manifestés dans des pratiques. Ce processus consiste à identifier des catégories d’objets et de traitement communes à des pratiques eﬃcaces, qui sont quant à elles spécifiques de situations, contextualisées et personnalisées. (J. Rogalski & Samurçay, 1994, p. 43)

La notion d’échantillon est un nouvel objet d’enseignement dans le programme de Seconde de 2009, même si cette notion était déjà présente comme thème d’étude possible dans le programme précédent.

Les termes « contenu », « capacités attendues » et « commentaires » font référence à la présentation classique des programmes en trois colonnes.

Elles précisent ensuite qu’il est nécessaire que ce savoir de référence puisse « s’expri-mer avec ses concepts, ses méthodes, ses systèmes de représentations et son langage » (ibid, p. 46).
Mais pour ce qui est des notions de logique, un tel savoir de référence n’existe pas au sens d’un corpus qui présente les caractéristiques listées ci-dessus et nous sommes dans une situation que décrit V. Durand-Guerrier dans l’introduction de son habilitation à diriger des recherches Recherches sur l’articulation entre la logique et le raisonnement mathématique dans une perspective didactique 4 :

Pratiquement absente aujourd’hui des curricula français, la logique à l’œuvre dans l’activité mathématique est également le plus souvent absente du dis-cours du professeur. Pour autant, les objets dont s’occupe la logique, tels que les connecteurs, la quantité, les règles d’inférences, la vérité et la validité sont autant d’outils de l’activité mathématique, utilisés le plus souvent de façon naturalisée, non problématisée et sans théorie de référence. (Durand-Guerrier, 2005, p. 5),

Cette absence m’amène à m’écarter un peu du chemin classique de l’étude du processus de transposition didactique, en introduisant un intermédiaire entre le savoir savant (la logique mathématique, mais qui n’est pas un savoir partagé par tous les mathématiciens) et le savoir à enseigner (tel que dessiné par les programmes actuels). Ma première question de recherche porte sur des caractéristiques épistémologiques (puisqu’il s’agit de construire un savoir) et didactiques (puisque ce savoir est intégré dans un processus de transposition didactique) d’un tel intermédiaire :

Quel savoir de référence serait épistémologiquement et didactiquement perti-nent pour l’enseignement de notions de logique au lycée ?

La constitution d’un savoir de référence est un processus collectif et long. À la suite d’une étude épistémologique et de travaux didactiques présentés dans une première partie de cette thèse, j’y apporterai ma contribution en proposant dans une deuxième partie une étude de diﬀérentes notions de logique. Je construis ainsi une référence qui m’est de toute façon nécessaire pour continuer l’étude du savoir à enseigner.

Titre intégral : Recherches sur l’articulation entre la logique et le raisonnement mathématique dans une perspective didactique. Un cas exemplaire de l’interaction entre analyses épistémologique et didactique. Apports de la théorie élémentaire des modèles pour une analyse didactique du raisonnement mathématique.

Même sans référence clairement définie, il y a aujourd’hui un savoir à enseigner, qui se trouve notamment dans les textes des programmes. Je poursuivrai ma recherche par une étude de ce texte du savoir, pour la rédaction duquel des choix ont été faits, que précise Y. Chevallard :

La production d’un système didactique à partir d’un projet social d’ensei-gnement préalable suppose la production d’un texte du savoir et cette mise en textes du savoir engendre les eﬀets énoncés précédemment (désyncrétisation 5, dépersonnalisation) tout en autorisant un rapport spécifique au temps didac-tique (programmabilité de l’acquisition du savoir). (Chevallard, 1985, p. 65)

Ma deuxième question de recherche concerne ce savoir à enseigner :

Quel est l’ensemble de conditions et de contraintes qui pèsent sur la transpo-sition didactique des notions de logique au lycée ?

Là aussi il y a une spécificité des notions de logique : j’ai déjà souligné que leur mention explicite était une nouveauté des programmes actuels et nous verrons que cela vient après une vingtaine d’années pendant lesquelles elles avaient été bannies des programmes, période qui faisait elle-même suite à celle des mathématiques modernes pendant laquelle elles étaient étudiées dans un chapitre spécifique (en lien avec la théorie des ensembles). Ces allers-retours ont empêché que des habitudes se prennent, qu’un discours se fixe et il n’y a pas plus de savoir de référence pour la logique à l’intérieur du système scolaire qu’à l’extérieur. L’étude du savoir à enseigner, avec une perspective historique, est l’objet de la troisième partie de cette thèse.

La formation des enseignants, troisième question de recherche

Dans ce contexte particulier d’absence pour certains enseignants de connaissances en logique mathématique, d’absence de savoir de référence institué par la communauté, de manque de stabilité sur le long terme du savoir à enseigner, nous pouvons légitimement nous interroger sur l’enseignement des notions de logique que les enseignants vont pouvoir mettre en place.

La formation des enseignants est un élément essentiel de la partie interne du processus de transposition didactique : le passage du savoir à enseigner au savoir enseigné. J’ai orienté la suite de ma recherche vers ces questions de formation. Les études des premières parties de la thèse me permettent d’identifier des besoins de formation et je proposerai ensuite l’analyse d’une formation particulière : un stage d’initiation à la logique proposé par l’Institut de Recherche sur l’Enseignement des Mathématiques (IREM) de Paris de-puis 2009, animé initialement par R. Cori. Ma troisième question de recherche porte sur cette formation mais reste dans la continuité de l’étude du processus de transposition didactique :

La formation permet-elle la constitution d’un savoir de référence utile aux en-seignants pour appréhender la complexité des notions de logique et les intégrer eﬃcacement dans leur enseignement ?

L’analyse du stage proposé en 2013 est l’objet de la quatrième partie de la thèse. Cette formation n’est pas une ingénierie que j’ai conçue : elle existait préalablement à ce travail. Cependant, son contenu se rapproche fortement de ce que j’aurais pu proposer comme scénario en m’appuyant sur les trois premières parties. Il est donc important de clarifier ma position pour l’analyse : d’une part je participe activement au stage en tant que formatrice, mais je prends une position distanciée pour l’analyser, d’autre part je regarde des choix de contenus qui ne sont pas les miens, mais auxquels j’adhère et que je cherche à argumenter par mes études épistémologique et didactique.

Choix méthodologiques

Je vais maintenant décrire l’itinéraire de ma recherche, qui suit les trois questions posées dans la problématique, en exposant la méthodologie adoptée pour y répondre. J’utilise le cadre d’analyse de la Théorie Anthropologique du Didactique pour décrire un processus de transposition didactique, mais je l’adapte aux spécificités de mon objet d’étude. Un tel processus s’inscrit dans le temps et son étude demande une prise en compte de la dimension historique, particulièrement importante ici puisque nous sommes dans un contexte de « ré-introduction » de notions de logique dans les programmes de lycée.

Nous avons vu dans la définition donnée en introduction que la logique, souvent présentée comme la science du raisonnement, participait aussi des sciences du langage. Je parle-rai alors de deux piliers de la logique : le langage et le raisonnement. Le pilier langage est cependant moins spontanément associé à la logique que le pilier raisonnement. C’est également un fil conducteur de ma thèse que de vouloir le réhabiliter. J’insisterai donc sur les questions de langage, au risque que ce soit au détriment du raisonnement. Dans cette optique, je considère que les notions de variable et de proposition sont essentielles. Malheureusement, le programme de 2009 n’en fait pas état. Ce que j’appelle par la suite notions de logique comprend aussi bien celle de variable ou de proposition que celles de connecteur, de quantificateur. . .

approches épistémologique et didactique

Je rassemble dans une première partie une étude épistémologique et une étude de tra-vaux didactiques car elles sont complémentaires dans la constitution d’une référence pour l’enseignement de notions de logique.

L’étude de systèmes logiques élaborés par diﬀérents philosophes ou mathématiciens, à dif-férentes époques, depuis la logique de l’Antiquité Grecque jusqu’à la constitution récente de la logique mathématique, permet d’envisager diﬀérentes conceptions 6 de la logique. Comme le souligne J-L. Dorier dans son habilitation à diriger des recherches Recherches en histoire et en didactique des mathématiques sur l’algèbre linéaire, perspective théorique sur leurs interactions :

Le sens des concepts, les problèmes qui s’y rattachent, la position relative d’un élément de savoir dans un savoir plus large qui l’englobe, mais aussi la variabilité de ces données en fonction des périodes et des institutions, etc. sont autant de questions qui aident a mieux comprendre le fonctionnement d’un système didactique. (Dorier, 1997, p. 9)

En étudiant ces systèmes avec une perspective historique, nous verrons ainsi l’évolution des notions de logique, en s’attachant dans les changements à en expliquer les raisons, les manques qui ont conduit à des modifications, ou au contraire ce qui est opérant et reste en place. Je retiens pour cette recherche trois périodes avec à chaque fois deux protagonistes qui reflètent deux prises de position presque contemporaines :

– l’Antiquité grecque avec Aristote et les Stoïciens (IVe, IIIe siècles avant JC),

– l’époque moderne avec Descartes et Leibniz (XVIIe, XVIIIe siècles),

– la naissance de la logique mathématique au XIXe siècle avec Boole et Frege.

Je choisis de privilégier deux axes pour cette étude, articulés avec mes questions de re-cherche :

– Le travail sur le langage.

– Le niveau de formalisation du langage et des raisonnements.

Plusieurs travaux de didactique des mathématiques ont déjà montré la pertinence de la logique des prédicats comme référence pour questionner l’enseignement de la logique des mathématiques. Je citerai notamment dans cette partie les travaux de V. Durand-Guerrier, dans lesquels une explicitation des démarches des élèves dans la résolution de certaines tâches, basée sur la logique mathématique, réduit la distance entre ce qui est appelée « logique de sens commun » et logique mathématique (c’est un axe fort de ses travaux que j’illustrerai à travers l’exemple de la tâche du labyrinthe).

J’étudierai ensuite une deuxième série de travaux didactiques, en relation avec la place du langage dans l’activité mathématique. Selon S. Epp, il faut une attention particulière pour que les étudiants acquièrent la maîtrise du langage suﬃsante pour l’activité mathématique :

The ability to rephrase statements in alternate, equivalent ways, to reco-gnize that other attractive-looking reformulations are not equivalent, and to have a feeling for truth and falsity of universal and existential statements are crucial mathematical problem-solving tools. Yet numerous studies show that students do not acquire these abilities spontaneously. 7 (Epp, 1999)

Je présenterai notamment la thèse de C. Laborde, Langue naturelle et écriture symbolique, deux codes en interaction dans l’enseignement mathématique, qui montre une spécificité du langage des mathématiciens. Mais ceux-ci ne se contentent pas d’utiliser deux codes, ils ont aussi pour une même proposition plusieurs formulations possibles, qu’ils utilisent selon les besoins de la situation. Je préciserai ensuite la notion de reformulation que je mettrai en lien avec la notion de registre de représentation sémiotique de R. Duval. Nous verrons enfin, à travers l’article Unpacking the logic of mathematical statements de A. Selden et J. Selden, l’importance de savoir mettre au jour la structure logique d’un énoncé pour organiser une démonstration ou contrôler sa validité.

proposition d’une référence pour l’enseigne-ment de notions de logique

Les études épistémologique et didactique nourrissent alors la réflexion sur la constitu-tion d’un savoir de référence concernant les notions de logique qui m’est nécessaire pour poursuivre l’étude. Dans cette deuxième partie, je ferai une présentation de diﬀérentes notions de logique adaptée à l’étude didactique qui est la mienne. Notamment, puisque je ne m’intéresse pas à l’enseignement de la logique mathématique, mais à l’enseignement de la logique des mathématiques, je m’appuierai sur l’activité mathématique, et plus particulièrement sur le discours mathématique, pour aborder ces notions.

Pendant plusieurs années, D. Lacombe a proposé dans le DEA de didactique des disciplines de l’université Paris 7 un Cours de logique élémentaire, dont le premier chapitre s’intitule Généralités sur le langage mathématique. Je m’en inspirerai largement pour introduire les notions d’expression mathématique, de variable muette et de signe mutificateur, de variable parlante, d’expressions synonymes. Les connecteurs et les quantificateurs seront ensuite présentés sous deux angles : une approche à partir la logique mathématique (on trouvera en annexe page 445 une présentation formelle des notions de base de la logique mathématique, comme cela peut-être fait dans un cours à l’université) et l’étude de leur ex-pression dans le discours mathématique. À travers ces deux approches, je cherche à éclairer les pratiques langagières 8 existantes, en les analysant à travers une grille de lecture fournie par la logique mathématique. Je les compléterai en donnant quelques résultats d’études didactiques. De la même manière, je m’appuierai sur la déduction naturelle pour étudier les diﬀérents types de raisonnement et expressions utilisées dans leur rédaction.

étude du savoir à enseigner

Les deux premières parties de cette thèse disent finalement d’où je regarde l’enseignement de la logique des mathématiques. Je vais maintenant préciser où je le regarde.

D’une certaine façon, une « heureuse circonstance » a orienté mon choix. En eﬀet, il y a eu récemment une modification dans les programmes de mathématiques pour le lycée concernant les notions de logique, visible à travers deux nouveautés : un tableau fixant des objectifs d’enseignement les concernant, des pages et des exercices qui leur sont consacrés dans les manuels. Il y a aujourd’hui une demande institutionnelle explicite, donnant une nouvelle dimension à l’étude de la transposition didactique. Il est ainsi possible de proposer l’étude d’un savoir à enseigner prenant en compte le programme et les manuels, qui sont une première mise en texte du savoir délimitant un espace de conditions et de contraintes pour l’enseignement.

L’analyse des programmes et des textes d’accompagnement avec une perspective histo-rique permet de voir diﬀérentes approches possibles des notions de logique. Pour cela, je m’appuierai sur les outils de l’analyse écologique, au sens de M. Artaud (Artaud, 1997) dans son cours à la IXe École d’été de didactique des mathématiques, pour voir où vivent les notions de logique et quelle fonction leur est attribuée. Je distinguerai 4 périodes :

de 1960 à 1969 : en 1960, la logique fait son entrée dans les programmes. Et dans les années qui suivent, des expériences sont faites sur le terrain en même temps que sont débattues certaines pratiques d’enseignement, notamment en ce qui concerne l’emploi des symboles logiques.

de 1969 à 1981 : c’est la période des mathématiques modernes. La logique est alors objet explicite d’enseignement. Mais cette réforme est rapidement l’objet de vives critiques.
de 1981 à 1999 : c’est la période de la « contre-réforme ». La logique, que certains ont associée au formalisme excessif reproché aux mathématiques modernes, en est exclue.

Le rapport de stage ou le pfe est un document d’analyse, de synthèse et d’évaluation de votre apprentissage, c’est pour cela clepfe.com propose le téléchargement des modèles complet de projet de fin d’étude, rapport de stage, mémoire, pfe, thèse, pour connaître la méthodologie à avoir et savoir comment construire les parties d’un projet de fin d’étude.

Table des matières

Introduction
Problématique et questions de recherche
Choix méthodologiques
I Approches épistémologique et didactique
1 Étude de différents systèmes logiques
1.1 L’Antiquité grecque : Aristote et les Stoïciens
1.2 L’époque moderne : Descartes et Leibniz
1.3 La naissance de la logique mathématique : Boole et Frege
1.4 Synthèse de l’étude épistémologique
2 Étude didactique
2.1 Pertinence de la logique des prédicats pour l’étude didactique
2.2 Le langage dans la classe de mathématiques
2.3 Synthèse de l’étude didactique
Conclusion des études épistémologique et didactique
II Proposition d’une référence pour l’enseignement de notions de logique
3 Notions de logique et étude du langage mathématique
3.1 Langage mathématique, discours mathématique, expressions mathématiques
3.2 Variable
3.3 Connecteurs ET et OU
3.4 Négation
3.5 Implication
3.6 Quantificateurs
3.7 Synthèse de l’étude du langage mathématique
4 Les raisonnements
4.1 Formalisation des démonstrations
4.2 Preuves dans le calcul des propositions
4.3 Implication et déduction
4.4 Introduction et élimination des quantificateurs
4.5 Divers types de raisonnement
4.6 Synthèse de l’étude des raisonnements
Conclusion sur la référence pour l’enseignement de notions de logique
III Étude du savoir à enseigner
5 Étude de la place de la logique dans les programmes de mathématiques pour la classe de Seconde depuis 1960
5.1 Analyse globale des programmes
5.2 Analyse par notion de logique des documents qui accompagnent les programmes
5.3 Synthèse de l’étude des programmes et documents d’accompagnement
6 Analyse des manuels
6.1 Analyse des pages « Logique » des manuels de Seconde
6.2 Analyse des exercices dans 5 manuels de 2010
Conclusion de l’analyse du savoir à enseigner
IV Analyse d’une formation continue « Initiation à la logique»
7 Les besoins de formation : analyse d’un questionnaire à destination des professeurs de Seconde
7.1 Modalités de passation du questionnaire
7.2 Caractéristiques générales des enseignants qui ont répondu
7.3 Mise en place d’un enseignement de notions de logique et notions travaillées dans la classe
7.4 Connaissances en logique mathématique et activités trouvées ou conçues pour atteindre les objectifs fixés par le programme
7.5 Recours à des ressources
7.6 Mise en forme de l’enseignement de notions de logique et institutionnalisation des connaissances
7.7 Des précisions sur l’institutionnalisation sur les connecteurs ET et OU
7.8 Synthèse du questionnaire et retour sur les besoins supposés
8 Analyse de la formation continue « Initiation à la logique »
8.1 Le scénario de la formation
8.2 Déroulement et analyse de la première journée du stage de 2013
8.3 Les activités présentées par les stagiaires
8.4 Bilan de la formation 2013
Conclusion de l’étude de la formation continue « Initiation à la logique »
Conclusion générale et perspectives
Études épistémologique et didactique
Proposition d’une référence pour l’enseignement de notions de logique
Étude du savoir à enseigner
Analyse d’une formation continue « Initiation à la logique »
Perspectives
Références
Liste des manuels scolaires étudiés
Programmes et documents d’accompagnement cités
Articles des bulletins APMEP cités
A Quelques notions de logique mathématique
A.1 Syntaxe et sémantique du calcul propositionnel
A.2 Syntaxe et sémantique du calcul des prédicats
A.3 Preuves formelles
A.4 Complétude et incomplétude
B Extraits de l’Organon d’Aristote
B.1 Extraits de Catégories
B.2 Extraits de De l’Interprétation
B.3 Extraits de Premiers analytiques
C Extraits de La logique de Port-Royal
C.1 Extraits de deux discours donnés en préambule
C.2 Préambule « Logique »
C.3 Extraits de la première partie
C.4 Extraits de la deuxième partie
C.5 Extraits de la troisième partie
C.6 Extraits de la quatrième partie
D Extraits des premiers chapitres de Les lois de la pensée, George Boole487
D.1 Extraits de l’introduction par Souleymane Bachir DIANE
D.2 Extraits du chapitre 1
D.3 Extraits du chapitre 2
D.4 Extraits du chapitre 3
D.5 Extraits du chapitre 4
E Extraits de l’Idéographie de G. Frege
E.1 Extrait de la préface
E.2 Extraits de la première partie
E.3 Extraits de la deuxième partie
F Extraits de textes et programmes officiels
F.1 Extraits des instructions du 19 juillet 1960
F.2 Extrait du commentaire du 6 février 1970
F.3 Extrait du programme de mathématiques pour la classe de Première littéraire, enseignement obligatoire au choix de 2004
G Sommaires des pages sur les notions de logique dans les manuels de 1969 et 2010
G.1 Manuels de 1969
G.2 Manuels de 2010
H Commentaires de certains exercices des manuels de 2010
I Questionnaire à destination des enseignants de Seconde
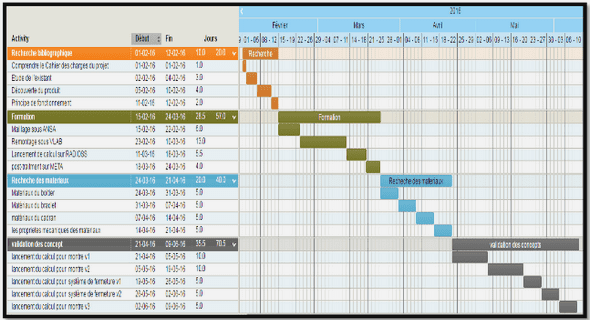
J Planning du stage 545
K Première journée du stage « Initiation à la logique 2013
K.1 Présentation de la formation
K.2 Test de début de stage
K.3 Exposé sur le langage mathématique
K.4 Exposé sur la structure modulaire du raisonnement mathématique, dialectique démonstrateur/utilisateur
K.5 Activités sur les connecteurs ET et OU au collège
K.6 Activité sur les théorèmes de Pythagore et de Thalès
K.7 Activités sur les connecteurs ET et OU en classe de Seconde
L Activités présentées par les stagiaires
L.1 Vrai ou Faux en Sixième
L.2 Vrai/Faux Troisième
L.3 Atelier Logique en Sixième
L.4 Activité circuit
L.5 Vrai/Faux en Seconde