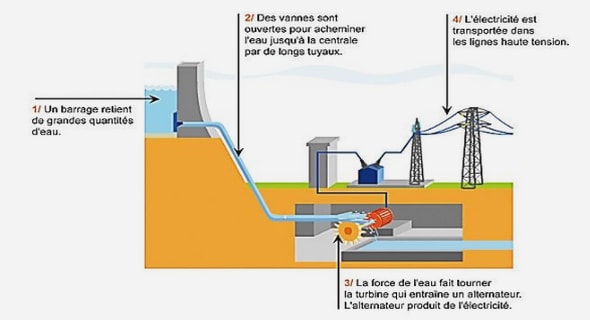
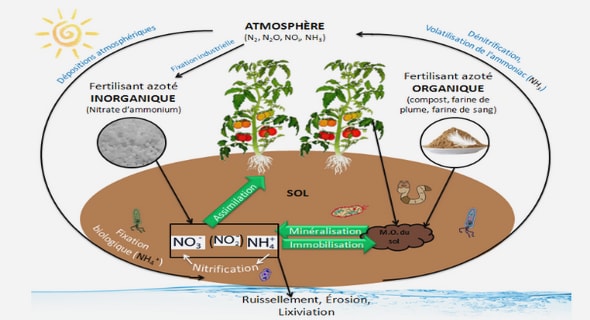
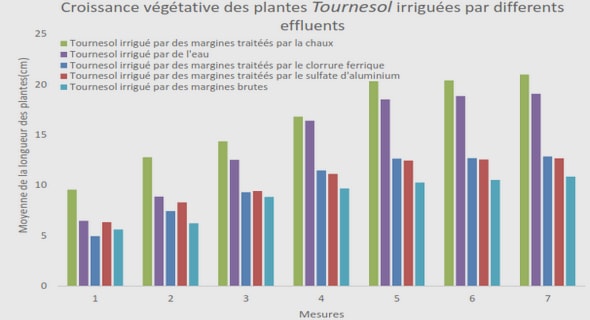
Télécharger le fichier pdf d’un mémoire de fin d’études
Analyse des outils existants
Les outils de correction topologique
Définition
Tout d’abord commençons par quelques définitions des couches qui seront utilisées et créées :
– Planches : il s’agit des feuilles (ex : K2, J3…) définies dans la partie 1.2.2
– L’enveloppe : il s’agit ici d’une triangulation de Delaunay ayant les mêmes caractéristiques qu’une enveloppe convexe, mais dont certains triangles ont été supprimés pour coller au mieux à la forme des planches (voir définition triangulation de Delaunay partie II.3)
– Trous et réseaux : les trous correspondent aux espaces vides entre les planches là où elles devraient normalement se toucher. Les réseaux correspondent aux espaces non cadastrés tels que les routes et rivières. Ils seront matérialisés tout deux par des polygones (pour plus de détails voir partie III.1).
La figure ci-contre montre les planches géoréférencées sans aucune correction topologique. Nous pouvons donc apercevoir les trous et recouvrement entre les deux planches ici en bleu et rose. Cette étape est primordiale pour éviter des erreurs avec les outils QGIS pour les étapes suivantes. Elle se réalise avec l’outil Vecteur/Outils de géométrie/Vérifier la validité. Après cette étape il faut corriger les géométries invalides si nécessaire. La plupart des erreurs relevées par cet outil sont dues à un mauvais nettoyage de la vectorisation automatique (sommets en double…) et peuvent être corrigées automatiquement à l’aide d’outils QGIS 3.0.
Etape 2 : Intersection des planches
Ici nous allons récupérer les intersections des planches entre elles en créant une nouvelle couche de polygones issus de cette intersection. Cette couche nous servira par la suite pour effectuer une requête spatiale et détecter les chevauchements. Pour effectuer cette opération il faut utiliser l’outil Vecteur/Outils de géotraitement/Intersection. L’opération est à répéter autant de fois qu’il y a de planches qui s’intersectent. Par la suite nous allons réunir toutes les intersections dans une même couche avec l’outils Vecteur/Outils de géotraitement/Union. Il est possible que certaines géométries soient des multi-polygones alors qu’ils devraient être uniques, il faut donc utiliser l’outil Vecteur/Outils de géométrie/De morceaux multiples à morceaux uniques pour avoir un seul polygone par géométrie et ne pas avoir de multi-polygones. La sortie de cet outil est susceptible de contenir des doublons, c’est pourquoi il faut utiliser l’outil Supprimer les géométries dupliquées.
Etape 3 : Recherche des superpositions
Par la suite, il faut unir toutes les planches de la même année entre elles avec l’outil Union utilisé précédemment. La couche en sortie est de nouveau susceptible de contenir des géométries en double, il faut donc les supprimer avec l’outil Supprimer les géométries dupliquées. Ensuite, il faut effectuer une requête spatiale où l’union des planches contient, est égal ou est à l’intérieur des superpositions. Nous choisissons tous ces critères pour ne pas oublier de polygones, en effet normalement, le critère d’égalité devrait suffire à lui seul, mais à cause des différentes manipulations effectuées en amont, il y a des micro-erreurs qui se sont glissées dans nos polygones. C’est pourquoi nous choisissons ces 3 critères.
Etape 4 : Suppression des trous
Une fois les superpositions sélectionnées grâce à la requête spatiale, nous pouvons les fusionner avec un polygone voisin (plusieurs options sont proposées pour la fusion : avec le polygone le plus grand, avec le polygone le plus petit, avec le polygone ayant la plus grande frontière en commun) avec l’outil Vecteur/Outils de géotraitement/Supprimer les débordements (2.18) ou Supprimer les polygones sélectionnés (3.0)
Ici nous retrouvons le résultat de la première partie de la chaîne de traitement. Les chevauchements ont été corrigés. A la sortie de cette partie, il est possible d’avoir des parcelles en double, il faudra alors les nettoyer manuellement (voir partie IV, analyse des résultats). Il ne reste plus que les trous entre les planches.
|
Table des matières
TABLE DES MATIERES
INTRODUCTION
I CONTEXTE ET DONNEES
I.1 LA CHAINE DE TRAITEMENT ELABOREE PAR LE LABORATOIRE GEF
I.2 LES DONNEES
I.2.1 Aspects généraux
I.2.2 Les données utilisées
I.3 ANALYSE DES OUTILS EXISTANTS
II ASPECTS THEORIQUES
II.1 TOPOLOGIE
II.1.1 Les relations topologiques
II.1.2 Les outils de correction topologique
II.2 LA THEORIE DES GRAPHES
II.2.1 Histoire des graphes
II.2.2 Définition
II.2.3 Projets utilisant la théorie des graphes
II.3 OUTILS D’ANALYSE
III METHODOLOGIE
III.1 NOTIONS DE RELATIONS ENTRE LES DIFFERENTES ENTITES
III.2 MOSAÏQUAGE
III.2.1 Présentation du traitement
III.2.2 Suppression des chevauchements
III.2.3 Suppression des trous
III.3 APPLICATION DE LA THEORIE DES GRAPHES
III.3.1 Différents types de graphes
III.3.2 Traitement d’une planche
III.3.3 Graphe de plusieurs planches
IV PRESENTATION DES RESULTATS
IV.1 LES RESULTATS DU MOSAÏQUAGE
IV.1.1 Année 1813
IV.1.2 Année 1850
IV.1.3 Années 1972-1974
IV.2 LES RESULTATS DES GRAPHES
IV.2.1 Année 1813
IV.2.2 Année 1850
IV.2.3 Année 1973
IV.3 LIENS ENTRE MOSAÏQUAGE ET THEORIE DES GRAPHES
CONCLUSION ET PERSPECTIVES
BIBLIOGRAPHIE
Télécharger le rapport complet