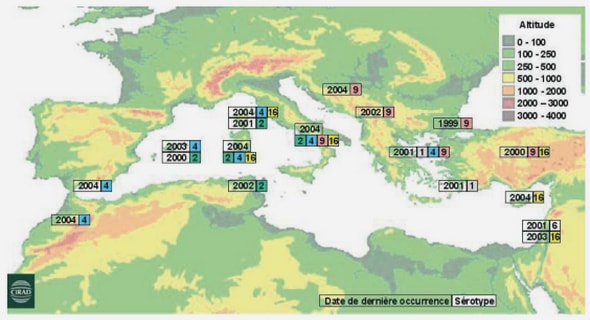
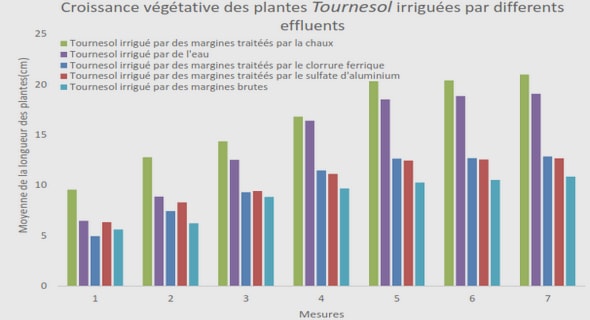
Etude exp´erimentale de structures membranaires `a autocollimation

Télécharger le fichier pdf d’un mémoire de fin d’études

L’autocollimation parfaite

Quelle geometrie l’isofrequence doit-elle avoir pour produire une autocollimation \par-faite »? Avant tout, qu’entend-on par autocollimation parfaite pour un faisceau monochro-matique ? L’autocollimation parfaite correspond a une propagation du faisceau sans la moindre modi cation de son pro l transverse ou, ce qui revient au m^eme, sans dispersion laterale de l’energie. En terme de courbe isofrequence, cela revient a dire que la normale a l’isofrequence pointe toujours dans la m^eme direction et ce pour tous les vecteurs d’onde qui composent le faisceau.

Approche graphique

La partie gauche de la gure I.13 page 20 contient les diagrammes de bande de trois milieux ctifs bi-dimensionnels aux proprietes dispersives di erentes : isotrope, anisotrope et autocollimatant. Sur chacun de ces diagrammes est representee la frequence reduite U = a= en fonction des directions de propagation dans le plan (kx,ky). est la longueur d’onde de l’onde consideree et a une taille caracteristique qui n’a ici pas d’importance particuliere. Nous nous interessons ici a une frequence reduite particuliere U0 pour comparer sa propagation dans chacun des trois milieux. Pour obtenir la courbe isofrequence a U0, il su t de considerer l’intersection entre le diagramme de bandes et un plan horizontal
U = U0. Les courbes isofrequences a U0 des trois milieux consideres sont representees a droite de la gure I.13 page 20, ainsi que certaines directions de propagation k et les vecteurs de Poynting correspondants P .
Pour le milieu isotrope, en haut de la gure, le diagramme de bandes est conique ce qui implique, sans surprise, que la courbe isofrequence a U0 est circulaire. On retrouve bien par consequent des directions de l’energie et de la phase identiques.
Au milieu de la gure, nous avons un diagramme de bandes representant un milieu anisotrope quelconque. L’isofrequence est une ellipse. Pour des vecteurs d’onde diriges selon les axes de l’ellipse, la phase et l’energie ont m^eme direction. Pour toutes les autres direc-tions de propagation, on constate que les directions de l’energie et de la phase di erent de facon plus ou moins grande. On remarque que cette ellipse presente autour de son petit axe une faible courbure. Dans cette zone, pour des vecteurs d’onde ayant des directions sensi-blement di erentes, les vecteurs de Poynting correspondants possedent tous des directions proches de l’axe ky. Dans un tel milieu anisotrope, un faisceau dirige selon le petit axe de l’isofrequence divergera plus lentement que dans un milieu isotrope (ou, ce qui revient au m^eme, l’etalement transverse de l’energie sera plus lent). Ce lien entre faible courbure et faible divergence va nous aiguiller vers la forme d’isofrequence qui permet l’autocollimation parfaite.
Le diagramme de bandes du bas est celui d’un milieu parfaitement autocollimatant. Ce diagramme se compose de deux plans inclines, symetriques par rapport au plan ky = 0 et qui se coupent en U = 0. L’isofrequence a U0 correspond ainsi a deux droites paralleles, toutes deux orthogonales a kx. On peut interpreter ce diagramme comme un cas limite d’anisotropie ou l’on fait tendre le grand axe de l’ellipse vers l’in ni (anisotropie extr^eme).
Cela signi e que, quel que soit k sur cette isofrequence, le vecteur P correspondant pointe toujours dans une m^eme direction qui est la parallele a l’axe ky. Il est a noter que tous les k sur cette isofrequence possedent la m^eme composante ky non-nulle. En outre, aucune propagation n’est possible selon kx. Dans un tel milieu, si on considere un faisceau mono-chromatique a U = U0 et se propageant selon ky, quels que soient son pro l transverse et sa divergence angulaire (c’est a dire sa distribution en kx), il se propagera sans dispersion laterale de l’energie.
On voit ici comment l’apparition d’une isofrequence plate permet de propager un faisceau ayant une certaine divergence angulaire (c’est a dire une extension non nulle dans l’espace des k transverses) sans etalement de l’energie.

Approche plus mathematique

Considerons le milieu autocollimatant parfait du bas de la gure I.13 page suivante ainsi que la propagation d’un faisceau monochromatique de frequence reduite U0. Ce fais-ceau se propage selon la direction ky entre les plans y = 0 et y = L. Soit E(x;0) le pro l du champ electrique de ce faisceau en y = 0, avec x la direction transverse et y la direction de propagation. Ce pro l peut se decomposer en une somme d’ondes planes de frequence spatiale kx : Z ~ ik x E(x;0) = E(kx) e x dkx (I.3) ou kx et ky sont lies par la relation U(kx;ky) = U0. Chacune des ondes planes composant ce faisceau se propage jusqu’en y = L en accumulant une phase ky L. Nous pouvons ainsi recomposer en y = L le pro l du faisceau propage en sommant chaque onde plane, a ectee du bon terme de phase : Z ~ ik x ik L E(x;L) = E(kx) e x e y dkx (I.4)

Cristal photonique a maille hexagonale

Avec le cristal photonique a maille hexagonale, l’autocollimation se produit pour une frequence reduite de U = 0;200 sur la premiere bande (voir la partie gauche de la gure I.14 page ci-contre) et une frequence reduite de U = 0;361 sur la deuxieme bande (voir la partie droite de la gure I.14 page suivante). Pour ces deux frequences, la courbe isofrequence reprend la forme generale du reseau reciproque et comprend notamment six zones relativement plates. Ces six zones correspondent a trois directions possibles pour l’autocollimation, avec a chaque fois deux sens possibles. Comme on peut le voir sur la gure I.15 page ci-contre, les trois directions d’autocollimation de la seconde bande sont tournees de 30 par rapport aux directions de propagation sur la premiere bande.

Cristal photonique a maille carree

Pour le cristal photonique a maille carree, l’autocollimation se produit a U = 0;201 sur la premiere bande et U = 0;289 sur la deuxieme bande (voir la partie gauche de la gure I.16 page 24). Une fois encore, aux frequences d’autocollimation, la courbe isofrequence reprend la forme generale du reseau reciproque et quatre zones plates apparaissent, correspondant a deux directions d’autocollimation avec deux sens possibles. Comme le montre la gure I.17 page 24, les deux directions d’autocollimation sur la premiere bande sont dirigees selon les diagonales du reseau carre, celles sur la deuxieme bande etant dirigees selon les c^otes du carre.

Choix de la maille

Comme nous le voyons ci-dessus, les deux mailles les plus simples nous permettent d’obtenir des directions d’autocollimation sur la premiere et la deuxieme bande. Cela nous laisse donc quatre possibilites parmi lesquelles choisir.
Tout d’abord, nous choisissons de travailler sur la premiere bande, ce qui elimine deux possibilites. Ce choix nous permet de nous placer en dessous du c^one de lumiere et de nous a ranchir des pertes de propagation par couplage aux modes de l’air. Comme nous souhaitons a terme realiser une cavite laser avec ce type de structure, il est en e et crucial de chercher a diminuer les pertes.

Inter^et de l’autocollimation pour le laser a semi-conducteur

Nous avons choisi dans la partie precedente le cristal photonique a maille carree a n d’etudier l’autocollimation. Nous avons obtenu au niveau de la premiere bande une courbe isofrequence qui presente un pro l carre. Une des ar^etes est perpendiculaire a Cela doit permettre d’obtenir un e et d’autocollimation dans la direction pour la frequence reduite UAC associee a l’isofrequence en question. Toutefois, cette geometrie d’isofrequence ne correspond pas a celle de l’autocollimation parfaite. Pour rappel, celle-ci est une droite ~ perpendiculaire a de nie pour tout l’espace k. Nous allons montrer dans cette partie que ce pro l est susceptible de fournir non seulement un guidage, mais aussi un ltrage spatial des modes guides par autocollimation. Cette propriet remarquable peut potentiellement corriger certaines limitations des techniques conventionnelles de guidage utilisees dans les lasers a semiconducteur. Nous rappellerons quelles sont ses limitations, et nous verrons comment l’autocollimation imparfaite que nous pouvons obtenir avec un cristal photonique peut permettre de les surmonter.

Les limites du guidage par contraste d’indice

Un laser de forte brillance est de ni par une qualite spatiale du faisceau exceptionnelle, ou reciproquement par un haut niveau de coherence spatiale dans le plan transverse. Pour atteindre de telles proprietes, le mieux est d’avoir une emission monomode laterale. Dans un guide par contraste d’indice classique ( bre ou guide a ruban par exemple), la densit laterale de mode est proportionnelle a la largeur du guide. Par consequent, pour conserver une emission monomode dans un laser a semiconducteur utilisant ce genre de guide, il faut limiter la largeur du guide en dessous d’une certaine valeur critique. Cela limite la surface disponible pour assurer le pompage du milieu gain. Pour augmenter la puissance emise par ces lasers, il est donc necessaire d’augmenter la densit de porteurs. Malheureusement cela introduit de nombreux e ets non-lineaires (anti-guidage, lamentation, …) qui degradent la qualite spatiale du faisceau. Dans les lasers a semiconducteur a guidage par contraste d’indice, il est donc di cile de concilier a la fois forte puissance et bonne qualite spatiale du faisceau. En d’autres termes, il est di cile d’obtenir des diodes laser de forte brillance. C’est une limitation des lasers a semiconducteurs par rapport a d’autres types de laser (solide, gaz ou bre).

Le guidage des modes en autocollimation imparfaite

L’autocollimation peut apporter une nouvelle approche pour concilier un regime de puissance et la qualite spatiale du faisceau. Nous allons en e et voir que l’autocollimation doit permettre de realiser des cavites qui favorisent un fonctionnement monomode spatial sur un mode fondamental de grande largeur. Il doit ^etre ainsi possible de monter en puis-sance non pas en augmentant la densit de porteurs, mais en augmentant la surface sur laquelle se fait l’injection de porteurs, evitant ainsi les e ets non-lineaires nefastes.

L’autocollimation parfaite, presentee a la partie I.4 page 18, garantit une propagation a l’in ni d’un mode en preservant son pro l transverse, quel que soit ce pro l. Dans ce cas, aucun processus ne vient favoriser un pro l de mode particulier. Tout mode ayant la bonne frequence se propagera identique a lui-m^eme, quelle que soit sa decomposition en somme d’ondes planes (equation I.6 page 21). Il n’y a aucune selectivit spatiale et par consequent l’autocollimation parfaite n’o re aucune avancee par rapport au guide par contraste d’indice.

En revanche, l’autocollimation \imparfaite » que nous obtenons avec le cristal pho-tonique a maille carree est de nie par une autocollimation valable uniquement pour une k ~ k certaine gamme angulaire kAC centree sur l’axe Cette caracteristique nous pro- cure un ltrage spatial par l’intermediaire de deux e ets susceptibles de favoriser les modes fondamentaux de grande etendue:

Le premier est lie a la presence des zones de superprisme et de bande interdite sur l’isofrequence a UAC . Decomposons en une somme d’ondes planes un mode se propageant le long de l’axe Ses frequences spatiales sont comprises dans un certain intervalle ~ k kk centr sur l’axe . Nous avons deux possibilites :

1.~~ k kk k kAC k, ou

2.~~ k kk k kAC k.

Comme indique sur la gure I.19 page 28, l’e et du cristal photonique sur les composantes ~

E(k) va dependre de la zone dans laquelle elles se situent. Dans le premier cas, les compo-santes se propagent integralement sans se deformer et sans se dephaser les unes par rapport aux autres : le faisceau est autocollimate. Dans le second cas, les composantes en dehors de k ~ k l’intervalle kAC sont ltrees et ne se retrouvent plus dans le pro l du faisceau propage : soit elles ont et fortement deviees par e et superprisme, soit elles n’ont pas pu se propager car situees dans la bande interdite. On elimine ainsi les hautes frequences spatiales du mode propage. Ceci pourrait permettre de lisser un mode faisant appara^tre des points chauds ou de l’automodulation.

Le deuxieme e et est lie a la courbure residuelle qui existe pour k kk k kAC k. En e et, nous avons signale que l’isofrequence UAC n’est pas parfaitement rectiligne sur tout j ~ k l’intervalle kAC . La courbure residuelle tend a legerement disperser le faisceau. Cet e et est d’autant plus marque que la decomposition du faisceau E(k) est large en k. Un mode transverse large, c’est a dire ayant une decomposition resserree autour de k = 0, sera donc moins dispers qu’un mode spatialement etroit. L’autocollimation imparfaite tend donc a favoriser les modes transverses ayant la decomposition en k la plus resserree possible : il s’agit des modes spatialement large et dont le pro l est le plus « doux »possible, c’est a dire ayant le moins de noeuds. Elle permet donc d’assurer un certain ltrage spatial qui favorise les modes transverses fondamentaux et les plus etendus possibles. Cela est particulierement interessant pour la conception de laser de forte brillance.

Concernant le ltrage spectral, les frequences autour de UAC presentent des courbures faibles, mais non-nulles. Pour U < UAC , la courbure est convexe. Pour U > UAC , elle est concave. Dans les deux cas, le mode diverge au cours de sa propagation car il n’y a pas d’autocollimation.

Nous avons donc un cristal photonique qui a priori favorise les modes larges, mo-nolobes, et de frequence UAC . La question qu’il faut se poser maintenant est celle du dimensionnement de la cavite que l’on peut concevoir avec un tel cristal photonique et plus particulierement le guide a autocollimation qui constituera le c ur de cette cavite. En particulier, pour une largeur de mode transverse donnee, quelle longueur de guide faut-il considerer ? Il faut aussi savoir si l’e et de ltrage spectral sera su sant pour assurer un fonctionnement monomode longitudinal ou s’il sera necessaire de recourir a un autre phenomene de ltrage spectral.

Presentation de la structure membranaire

La cavite tout cristal photonique a autocollimation sera realisee sur une membrane GaAs suspendue dans l’air. Une illustration de cette membrane est representee sur la gure II.1. Les membranes dont nous disposons ont des epaisseurs comprises entre 150 et 350 nm. Elles contiennent des puits quantiques GaInAs qui emettent selon la polarisation TE (champ electrique dans le plan de la membrane) dans des gammes de longueur d’onde situees entre 960 et 1020 nm. La membrane fait o ce de guide vertical a fort con nement pour l’onde emise par les puits quantiques.

La membrane peut ainsi se ramener a un materiau planaire d’indice e ectif ne pour la polarisation d’inter^et. Cet indice est fonction de l’epaisseur de la membrane, de l’indice du materiau composant la membrane, ainsi que de la longueur d’onde d’emission. La gure II.2 page ci-contre montre la variation de l’indice e ectif en fonction des indications citees plus haut (membrane GaAs d’epaisseur comprise entre 150 et 350 nm et emettant entre 960 et 1020 nm). Nous relevons d’apres cette gure un encadrement de l’indice e ectif entre 2,86 et 3,37 pour l’ensemble des membranes dont nous disposons.

Sur cette membrane, nous allons realiser un cristal photonique constitue de trous de rayon r arranges selon un cristal carre de maille a. Pour ce cristal, le parametre pertinent est le rapport r=a qui va ^etre contraint par les limitations technologiques liees a la fabrication du cristal photonique. Lors de la fabrication, le rayon r des trous ainsi que la distance minimale entre trous d = a 2r doivent rester superieurs a des valeurs limites. Il n’est ainsi pas possible au laboratoire de graver des trous de rayon inferieur a r0 = 40 nm et qui traversent toute l’epaisseur de la membrane, notamment a cause des e ets ARDE 1

[43] qui tendent a faire diminuer la vitesse de gravure quand le rayon diminue. De m^eme, pour la distance d, il est tres di cile de descendre en dessous de d0 = 50 nm a cause des e ets de proximite lors de l’insolation electronique et lors de la gravure. Comment ces deux limitations sur r et d vont nous permettre d’etablir un encadrement du rapport r/a, qui est le parametre de conception pertinent pour le cristal photonique ?

Globalement, pour des indices e ectifs compris dans la gamme 2,86 a 3,37, la frequence reduite d’autocollimation se situe entre 0,15 et 0,25 (a= )[44]. En prenant une emission des puits centree a 1000 nm, le parametre de maille a se situe entre 150 et 250 nm. La gure II.3 indique l’evolution de la distance minimale d en fonction du rayon des trous pour les trois parametres de maille suivants : 150, 200 et 250 nm. Dans les zones grisees, les contraintes technologiques sur r ou sur a ne sont pas respectees. Dans la partie res-tante, nous pouvons choisir librement le rapport r=a. On peut ainsi le faire varier entre un minimum de r=a = 40=250 = 0;16 et un maximum de r=a = 100=250 = 0;4. Nous pouvons ainsi couvrir une gamme de r=a comprise entre 0;16 et 0;4.

Nous venons de determiner les gammes de l’indice e ectif et du rapport r/a pour notre etude theorique de l’autocollimation sur un cristal photonique a maille carree. A n de mieux etudier le comportement de l’autocollimation, nous choisissons de legerement elargir ces gammes,et nous prendrons nalement pour l’indice e ectif un encadrement des valeurs entre 2,8 et 3,4 et pour le rapport r/a un encadrement des valeurs entre 0,15 et 0,45.

Methode de determination de la frequence reduite d’au-tocollimation

Pour mener a bien le dimensionnement du cristal photonique a autocollimation il nous faut faire une etude parametrique de l’e et d’autocollimation. Pour cela, nous devons disposer d’une methode permettant de determiner la frequence d’autocollimation pour un jeu de parametres donnes. En outre, nous souhaitons conna^tre par la m^eme occasion l’acceptance angulaire de l’autocollimation. En d’autres termes, nous devons determiner l’isofrequence la plus plate parmi toutes les isofrequences de la bande consideree, determiner la frequence reduite associee UAC ainsi que la gamme de vecteurs d’onde kAC sur laquelle l’isofrequence est plate. Cette isofrequence ne peut pas ^etre determinee « visuelle-ment », car il n’y a pas de saut abrupt lors du passage par la frequence d’autocollimation : on passe continument et lentement d’une courbure locale positive a une courbure negative (voir par exemple la gure I.16 page 24). Nous avons donc mis au point une methode nu-merique simple et repetable pour determiner la courbure (ou plut^ot l’absence de courbure) sur les di erentes isofrequences considerees. Le principe de cette methode est de parcou-rir chaque isofrequence et de mesurer la gamme angulaire k dans laquelle la normale a l’isofrequence reste sensiblement parallele a la direction d’autocollimation. L’isofrequence presentant la gamme k la plus large est consideree comme l’isofrequence d’autocollima-tion : sa frequence est la frequence d’autocollimation UAC et la gamme angulaire kAC donne l’acceptance angulaire de cette autocollimation.

Considerons l’exemple suivant pour illustrer l’utilisation de cette methode. On s’interesse a la premiere bande du diagramme de dispersion U(k) d’un cristal photonique carre constitue de trous d’air dans un materiau d’indice e ectif ne = 2;9, de maille a, de rapport r=a = 0;3, et ce pour une polarisation T E. Ces valeurs sont les valeurs typiques pour une membrane GaAs de 150 nm d’epaisseur, emettant a 1000 nm (voir gure II.2 page 35).

Nous determinons le diagramme a l’aide du programme de calcul d’ondes planes MPB (MIT Photonic Band[41]). Ce logiciel fournit pour tout point (kx; ky), non seulement la frequence reduite U, mais aussi la vitesse de groupe VG qui est proportionnelle a la normale a l’isofrequence en ce point.

Sur la partie gauche de la gure II.4 page suivante, nous avons represent dans l’es-pace (kx; ky) 10 isofrequences de la premiere bande du diagramme de dispersion. Nous avons ajoute pour quelques points sur ces isofrequences la direction de la vitesse de groupe VG ( eches noires). Dans la region indiquee en gris clair (qui se situe autour de U = 0;2), la courbure des isofrequences diminue puis change de signe. Dans cette region, les isofre-quences presentent des portions relativement plates, et les vitesses de groupe sont quasi-ment toutes dirigees dans la direction C’est dans cette region que se situe la frequence d’autocollimation UAC .

La determination, pour une isofrequence donnee, de la gamme angulaire k autour de dans laquelle l’isofrequence est plate se deroule de la maniere suivante :

1. On part du point de l’isofrequence qui se trouve dans la direction d’autocollimation (dans le cas present ce point est situe a l’intersection entre et l’isofrequence etudiee).

2. En chaque point, on compare la direction d’autocollimation avec celle de la vitesse de

3.~ ~groupe. Pour cela, on projette la vitesse de groupe sur une base orthonormee N ; T~ ou N pointe dans la direction d’autocollimation. Nous considerons alors le rappor~ VT (k)=VN (k) entre les composantes tangentielle et normale de la vitesse de groupe.

Si ce rapport est nul, la vitesse de groupe (ou ce qui revient au m^eme la normale a l’isofrequence) pointe dans la direction d’autocollimation N.

3. Tant que la normale a l’isofrequence reste parallele a la direction d’autocollimation, on est toujours a l’interieur de la gamme k et on continue a se deplacer le long de l’isofrequence.

Le rapport de stage ou le pfe est un document d’analyse, de synthèse et d’évaluation de votre apprentissage, c’est pour cela clepfe.com propose le téléchargement des modèles complet de projet de fin d’étude, rapport de stage, mémoire, pfe, thèse, pour connaître la méthodologie à avoir et savoir comment construire les parties d’un projet de fin d’étude.

Table des matières

Remerciements
INTRODUCTION
I Autocollimation dans les cristaux photoniques
I.1 Introduction
I.2 Etat de l’art des cristaux photoniques `a autocollimation
I.2.1 D´eveloppement
I.2.2 Applications
I.2.3 Bilan
I.3 Propagation de la lumi`ere dans un milieu anisotrope
I.4 L’autocollimation parfaite
I.4.1 Approche graphique
I.4.2 Approche plus math´ematique
I.5 Cristal photonique `a autocollimation
I.5.1 Choix du cristal
I.5.2 Propri´et´es du cristal photonique `a maille carr´ee
I.6 Int´er^et de l’autocollimation pour le laser `a semiconducteur
I.6.1 Les limites du guidage par contraste d’indice
I.6.2 Le guidage des modes en autocollimation imparfaite
I.7 Conclusion
II Conception de guides `a autocollimation
II.1 Introduction
II.2 Dimensionnement du cristal photonique
II.2.1 Pr´esentation de la structure membranaire
II.2.2 M´ethode de d´etermination de la fr´equence r´eduite d’autocollimation
II.2.3 Etude param`etrique de l’autocollimation
II.2.4 Choix du point de fonctionnement
II.3 Conception de guide `a autocollimation
II.3.1 Hypoth`eses de travail
II.3.2 Simulations FDTD
II.3.3 Mod`ele ondes planes
II.4 Conclusion
III Etude exp´erimentale de structures membranaires `a autocollimation
III.1 Introduction
III.2 Etude exp´erimentale de structure membranaire
III.2.1 Param`etres de la structure membranaire
III.2.2 Description de la structure de test
III.2.3 R´ealisation de la structure de test
III.2.4 Banc de caract´erisation
III.2.5 Mise en ´evidence des effets d’autocollimation
III.2.6 Conclusion
III.3 Etude d’un proc´ed´e de r´ealisation
III.3.1 Observation des ´echantillons r´ealis´es par le proc´ed´e de r´ef´erence
III.3.2 Lib´eration de la membrane
III.3.3 Am´elioration du masque de silice
III.3.4 Etude des conditions de gravure de la membrane
III.3.5 Passivation des d´efauts de surface
III.4 Conclusion
CONCLUSION
Annexe
A Simulations FDTD de guides `a autocollimation
B Gravure du GaAs
B.1 Rappel sur les m´ecanismes de gravure plasma RIE
B.2 Analyse param´etrique de la gravure du GaAs en mode ICP-RIE
B.2.1 Puissance plasma
B.2.2 Puissance de polarisation
B.2.3 Pression
B.2.4 Les gaz
B.2.5 Suscepteur
B.2.6 Temp´erature
C Mod`ele balistique de gravure
D Passivation ´electronique
D.1 Th´eorie
D.1.1 Recombinaison indirecte : mod`ele de Shockley-Read-Hall
D.1.2 Recombinaison de surface : mod`ele de Stevenson-Keyes
D.2 Recombinaisons de surface : GaAs, InP
D.3 Principe de la passivation ´electronique
D.4 Action du solvant dans la passivation soufre du GaAs
Bibliographie

Télécharger le rapport complet

L’autocollimation parfaite

Approche graphique

Approche plus mathematique

Table des matières

Vous pourriez aussi aimer :

Laisser un commentaire Annuler la réponse