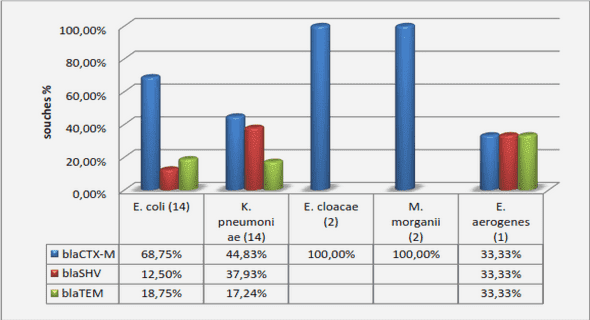
Commande par invariance d’une classe de systèmes de convolution

Télécharger le fichier pdf d’un mémoire de fin d’études

Sur les systèmes logistiques

La notion de système ou de chaîne logistique remonte au début des années 50 où le concept de la logistique était limité au domaine militaire. Depuis le 18ème siècle, la lo-gistique fut appliquée dans le milieu industriel pour la manutention et le transport des marchandises [Journet (1997)]. En eﬀet, Archimède était le premier scientifique qui a évo-qué le problème de la logistique, en cherchant à optimiser le déplacement des troupes de masses énormes d’infanterie, d’éléphants et de cavalerie. Ce concept n’a cessé d’évoluer, en recouvrant aussi bien les opérations d’achat et d’approvisionnement, que les fonctions de gestion commerciale et de distribution. Cette évolution s’est naturellement accompagnée de diﬀérentes définitions des systèmes et chaînes logistiques. Notre analyse de cette littérature montre qu’un système logistique se définit par le proces-sus d’obtention d’un produit fini ainsi que les diﬀérents acteurs en charge de ce processus. En eﬀet, selon le « SCC » 1, un système logistique peut être défini comme étant « la suite des étapes de production et de distribution d’un produit depuis les fournisseurs des four-nisseurs du producteur jusqu’aux clients de ses clients ». Cette définition met en avant le produit, de telle façon que le système logistique est perçu comme une succession de processus assurant les fonctions d’approvisionnement en matières premières, de transfor-mation de ces matières en composants et produits finis, et de distribution de ces produits vers les clients finaux, sans distinction notable entre les entités en charge de ces opérations [Lee et Billington (1993)].
D’un autre point de vue, un système logistique peut être défini comme un système global d’entités, constitué de sous-traitants, de producteurs, de distributeurs, de détaillants, et de clients, entre lesquels s’échangent diﬀérents flux de matière et d’informations. Cette définition, qui conserve les activités liées à l’élaboration du produit, fait apparaître les en-tités comme acteurs majeurs du système global, et met en avant la notion de flux comme lien entre ces entités [Tayur et al. (1999)].
Les diﬀérentes définitions présentées, qui s’agissant d’amener un produit fini au consom-mateur final, donnent une vision générale du système logistique. Elles se situent à un niveau d’abstraction qui n’oﬀre pas de détails sur la structuration des éléments qui com-posent le système, et les interactions qui gouvernent sa dynamique. Dans ce contexte, la structure des systèmes logistiques dépend essentiellement de la complexité du secteur d’activité, et des diﬀérents procédés de fabrication. Chaque entité du système logistique joue un rôle précis dans le processus global de l’obtention du produit fini. Ces entités, qui peuvent comporter soit des fournisseurs, des producteurs, des distributeurs, ou des consommateurs finaux, sont appelés maillons, échelons ou encore niveaux du système lo-gistique. En eﬀet, les diﬀérents échelons du système logistique sont reliés et interagissent entre eux moyennant un échange de trois types de flux : les flux physiques, les flux de données et les flux financiers.
Le flux physique, ou flux de matière, représente le cheminement de la matière phy-sique dans le système logistique, et le traverse essentiellement des fournisseurs vers les clients, comme l’illustre la figure 1.1. Il comporte aussi bien les matières pre-mières brutes que les composants et les encours, ainsi que les produits finis. Le mouvement de ce flux est gouverné par la succession des opérations de transfor-mation ou de production, de stockage et de distribution des produits.
Le flux de données englobe l’ensemble des données que s’échangent les diﬀérentes parties d’un système logistique, et qui se distinguent en deux sortes. Le flux infor-mationnel comprend toutes les données commerciales concernant les commandes passées par les clients, et les informations techniques de l’entreprise, telles que la capacité de production et de stockage. Quant aux flux décisionnels, ils résument les décisions prises par les centres de gestion, comme par exemple les ordres de production, d’approvisionnement et les consignes du stock.
Le flux financier concerne toutes les transactions pécuniaires qui ont lieu au sein du système logistique. Ce flux traverse la chaîne essentiellement d’aval en amont, et se présente comme la contre-partie monétaire du flux physique. Dans le cadre de cette thèse, seuls les flux physiques et informationnels sont considérés.

Enjeux de la gestion des systèmes logistiques

La gestion des systèmes logistiques consiste en un ensemble de management et d’op-timisation visant à gérer et à coordonner toutes les entités du système logistique. Nous citons les méthodes de calcul des besoins, connues sous l’acronyme MRP pour Material Requirements Planning, les méthodes de gestion dite Kanban ou juste à temps, les poli-tiques de gestion sur stock pS, sq et pQ, rq, et la politique connue sous l’acronyme CONWIP pour Constant Work-In-Process. Ces méthodes classiques de gestion développées dans la littérature portent essentiellement sur le pilotage des flux physiques des matières et des produits, à travers la maîtrise des diﬀérents processus logistiques tels que la production, l’approvisionnement, le stockage et le transport. Dans ce sens, l’objectif de chaque entre-prise revient en premier temps à fixer ses indicateurs de performance, pour construire un système logistique qui lui permette d’augmenter les profits et de diminuer les pertes. Dans ce qui suit, nous citons les principaux indicateurs de performance fixés par les entreprises.

Indicateurs de performance

Pour la gestion d’un système logistique fiable, il convient de définir des outils d’analyse appropriés, pour mesurer de façon précise, l’eﬃcacité et la performance du système. Ces mesures ou critères de performance peuvent être de natures qualitatives et quantitatives. Les mesures qualitatives ne sont pas numériquement mesurables, et englobent la satisfac-tion de la demande des clients, la flexibilité de la chaine logistique en cas de fluctuation de la demande, ainsi que le degré de minimisation des pertes encourus par chaque entité du système. Quant aux mesures quantitatives, elles sont descriptibles numériquement, comme par exemple le taux de minimisation de coûts, la maximisation des ventes et des profits, et la stabilité du niveau de référence du stock.

Dans ce contexte, la maîtrise des stocks est un point essentiel. Le stock est en eﬀet la ressource critique car les autres indicateurs dépendent plus ou moins de sa dynamique d’évolution. La diﬃculté de la gestion des stocks réside dans le fait de garantir un taux de prestation le plus élevé possible, et d’avoir un coût de possession le plus faible possible. Le premier impose la nécessité d’avoir des stocks les plus réactifs pour répondre de façon idéale à la demande, ce qui présente un coût de détention conséquent et un risque de désuétude des marchandises stockées. En contre-partie, le second exige de minimiser les stocks au niveau le plus bas possible, le risque étant de ne pas pouvoir répondre à la demande ce qui explique le paradoxe. En eﬀet, la gestion des systèmes logistiques vise à maintenir un équilibre entre les quantités stockées, nécessaires pour garantir un bon taux de service, et les coûts qui peuvent en être engendrés.

Dans les travaux de cette thèse, les enjeux et les objectifs globaux de gestion de systèmes logistiques portent sur la planification de la production et la gestion des stocks. Nous nous intéressons en particulier aux décisions de gestion de la production, afin de satisfaire les demandes des clients non connues et variables, et de maîtriser les niveaux de référence des stocks. Concrètement, nous proposons des solutions de configuration des ressources du système, à travers le dimensionnement des ressources de stockage et de production. Ces solutions peuvent être utilisées lors de la phase de conception des structures, pour déter-miner les performances exigées telles que la stabilité du stock, la satisfaction des clients, et les profits économiques. En outre, il faut noter que toute variation de la demande finale peut engendrer des variations de plus en plus importantes à chaque niveau en amont du système logistique. Ce phénomène de propagation de variations, connu sous le nom de « Bullwhip eﬀect », est introduit dans la section suivante.

Facteurs de variabilité et eﬀet « Bullwhip »

La complexité de la gestion du système logistique est appuyée par la présence d’in-certitudes et des variations qui touchent le système avec des erreurs d’estimation et de transmission de données d’une part, et les pannes et autres aléas de production d’autre part. Les deux grands facteurs de variation sont principalement la demande du client, et les délais ou retards d’obtention du produit fini.

La demande du client est le point de départ de la tâche de gestion des systèmes logis-tiques. Plusieurs techniques d’estimation et de prévision de la demande sont utilisées pour prédire au mieux possible les changements du marché. Malgré cela, ces techniques de pré-vision échouent, et souvent le marché visé est instable car la demande est changeante et incertaine.

L’autre facteur qui est le délai, est présent intrinsèquement dans tous les processus logis-tiques, comme par exemple les délais des échanges d’information et de prise de décision, les retards de production et les temps de transport. Les retards ne peuvent être réduits au-deçà d’un temps donné nécessaire à l’exécution de ces opérations, et constituent alors un indicateur de performance pour le système logistique considéré. De même, la connais-sance exacte de ces délais est une opération délicate et critique, puisqu’ils dépendent de facteurs extérieurs, tel que l’état des routes pour la distribution, le facteur humain dans la production et la décision, ainsi que les retards liés aux pannes et autres aléas rencontrés. Ces éléments et leur non prise en compte contribuent à l’apparition d’un phénomène connu sous le nom de « Bullwhip eﬀect » ou « Eﬀet Forrester », pouvant provoquer l’instabilité du système logistique. Cette appellation a été popularisée par [Lee et al. (1997)], mais elle remonte aux travaux [Forrester (1958), Forrester (1973)].

Ce phénomène correspond à l’amplification de la variation de la demande, et sa pro-pagation le long d’une chaîne logistique, du client consommateur vers le fournisseur de matière première. Les oscillations croissantes propageant dans le sens inverse du flux phy-sique illustré par la figure 1.1, entrainent une surproduction et donc un excès de stock, et par conséquent, pour éliminer ce surplus, les ordres de production sont revus à la baisse provoquant une nouvelle variation et ainsi de suite d’un échelon à un autre. Des travaux récents concernent les méthodes et outils de modélisation des systèmes logistiques, pour lutter contre ce problème typique [Wang et Disney (2016)]. En eﬀet, la section suivante est dédiée à la synthèse de l’état de l’art des études des systèmes logistiques.

Étude des systèmes logistiques

Les outils de modélisation et de planification de la production au sein des systèmes logistiques, permettent aux entreprises d’anticiper leurs réactions, et d’évaluer l’agilité de leurs organisations face aux dynamiques des marchés. En premier lieu, nous présentons un état de l’art des travaux théoriques et industriels existants, afin de mieux cerner les outils de modélisation mis en œuvre. En second lieu, nous nous intéressons aux modèles de gestion de stock, qui représentent la trame de départ de nos travaux de recherche.

Modèles et outils de modélisation

Dans la littérature, plusieurs taxonomies de méthodes utilisées pour modéliser la dyna-mique des systèmes logistiques sont proposées. Une première typologie initiée par Beamon dans [Beamon (1998)], classifie les modèles selon le type d’approche considérée et l’objectif visé pour la modélisation du système. Nous distinguons alors des modèles déterministes, des modèles stochastiques, des modèles économiques et des modèles de simulation.

Les modèles déterministes sont des modèles mathématiques formels, souvent pré-sentés sous forme d’équations diﬀérentielles ou aux diﬀérences. Les modèles déter-ministes supposent que les variables et les paramètres du modèle sont connus avec certitude.

Les modèles stochastiques au contraire, supposent qu’au moins une variable du système est à caractère aléatoire ou probabiliste, et suit une loi de distribution sto-chastique donnée. Ces modèles permettent de quantifier les dynamiques du système logistique [Tayur et al. (1999)], en particulier celles des flux physiques.

Les modèles économiques se présentent souvent sous forme d’heuristiques déci-sionnelles, et abordent la dynamique des systèmes logistiques d’un point de vue action-réaction, entre le client et ses fournisseurs. Ces aspects font appel à la théorie des coûts de transaction et la théorie des jeux [Hennet et Arda (2008)], qui visent à étudier la dynamique du système logistique, et l’impact des décisions prises par chaque joueur participant.

Les modèles de simulation sont utilisés lorsqu’il est diﬃcile de décrire sous forme d’équation, les interactions entre les diﬀérentes variables des modèles analytiques. Ils sont l’alternative aux modèles analytiques, lorsque la résolution de ces derniers présente une grande complexité combinatoire, liée à la dimension du système étudié [Towill et al. (1992)]. Ces modèles oﬀrent l’avantage de pouvoir tester, hors ligne, diﬀérents scénarios et stratégies de gestion possibles, et d’étudier de façon « qualitative » les eﬀets des variations des paramètres du système.

Cette classification a été reprise plus tard dans [Min et Zhou (2002)], et étendue à deux autres catégories. Elle comprend d’une part, les modèles hybrides qui font appel à la foisaux approches déterministes et aux approches stochastiques, et les modèles connus par IT-driven models ou dirigés par les technologies de l’information d’autre part. C’est un domaine qui vise à améliorer la visibilité et la communication entre les diﬀérents maillons, par l’utilisation des systèmes d’information et des langages de programmation, tels que les logiciels GPAO pour Gestion de la Production Assistée par Ordinateur, et ERP pour Enterprise Resource Planning.

Une dernière taxonomie, proposée par Labarthe [Labarthe (2006)], introduit la classe de modèles organisationnels, à coté des modèles analytiques et de simulation présentés précédemment. Cette nouvelle classe de systèmes est basée sur des modèles multi-agents et des méta-modèles, pour représenter le système logistique global. En se basant sur les classifications présentées, nous nous intéressons dans le cadre de cette thèse, à la classe de modèles analytiques issue de la théorie du contrôle et systèmes asservis, que nous présentons dans la section suivante.

Modèles analytiques des systèmes logistiques

Les modèles analytiques représentent le système logistique selon une perspective quan-titative, associée à l’utilisation d’approches issues de la théorie de l’asservissement des systèmes ainsi que de la recherche opérationnelle, selon la figure 1.4.

L’application de cette théorie au domaine logistique, est due aux travaux de Simon [Simon (1952)] , prix Nobel d’économie en 1978, qui a constaté que la gestion des systèmes logis-tiques de production relève de l’automatique et de la régulation. La théorie du contrôle et des systèmes asservis consiste à modéliser le système logistique à partir d’équations diﬀérentielles, ou d’équations aux diﬀérences [Riddals et al. (2000)]. Cette modélisation permet d’étudier l’évolution dynamique du système en temps continu ou discret. Des struc-tures de commande de type feedback, ou rétroaction, sont mises en œuvre pour contrôler les système à temps continu et discret, et servent à étudier la stabilité de la structure commandée [Disney et Towill (2002)]. D’autres méthodes sont utilisées pour analyser les propriétés dynamiques, telles que les méthodes de contrôle robuste, de supervision, de contrôle optimal ou encore de contrôle prédictif [Sarimveis et al. (2008), Léchappé et al. (2015)].

De plus, des formalismes à événements discrets étudient les modèles de systèmes logis-tiques, en se basant sur l’occurrence d’événements significatifs, tels que l’arrivée de nou-velles commandes, ou l’occurrence des incidents et des aléas. Ceux-ci sont capables de faire basculer le système d’un état à un autre, ce qui les diﬀérentie des modèles continus. Nous citons les réseaux de Petri, l’algèbre des dioïdes et les systèmes (max,+)-linéaires, les chaînes de Markov et les réseaux de files d’attente, qui permettent de formuler les phé-nomènes de synchronisation et de parallélisme entre les ressources du système logistique. Comme nous l’avons déjà mentionné, les modèles analytiques sont souvent complétés par des études qualitatives de type simulation. En eﬀet, la dynamique des systèmes est l’une des méthodologies les plus importantes appliquées dans les modèles de simulation. Forrester [Forrester (1958), Forrester (1973)], a été à l’origine de nombreux travaux de modélisation des systèmes dynamiques et de la commande des chaînes logistiques. Le modèle est principalement décrit par des équations diﬀérentielles ou au diﬀérences, qui permettent d’étudier la dynamique d’évolution du stock, et de l’interpréter en termes des variables ou paramètres intervenant dans le système logistique, tels que la demande client, les retards et les rétroactions internes qui aﬀectent le comportement. Des travaux de re-cherche, tels que [Towill (1982), Edghill et Towill (1989), Wikner (2005)] ont mené à une famille de modèles génériques de gestion des stocks, appelés les modèles Inventory and Order-Based Production Control System connus par IOPBPCS, présentés dans la section suivante.

Méthodes de gestion des stocks

L’enjeu principal de la gestion des systèmes logistiques est souvent lié à la bonne maî-trise des niveaux de stockage, vu que la stabilité des stocks reflète l’état du système global. De ce fait, une mauvaise stratégie de gestion des stocks provoque des retards de livrai-son, une rupture du stock ou un sur-stockage, et des situations de pénurie qui influent directement sur la qualité de la production. Dans ce contexte, les recherches sur l’étude de la dynamique d’évolution des stocks, ont abouti au modèle connu dans la littérature sous l’acronyme APIOBPCS pour The Automatic Pipeline Inventory and Order Based Production Control System, et issu de l’approche des systèmes asservis et des modèles de simulation du type System Dynamics.

Ce modèle est omniprésent dans la littérature pour la gestion et la modélisation de la dynamique des chaînes logistiques. C’est une variante du modèle IOBPCS, qui est utilisé pour faire un balayage périodique du système de commande, afin d’adapter les ordres de production délivrés aux diﬀérentes demandes et aléas. Les prémisses du IOBPCS sont inspirées des travaux de Simon [Simon (1952)], qui a appliqué la théorie des servoméca-nismes sur la dynamique des systèmes logistiques de production. Il a décrit la relation entre les ordres de production délivrés et le niveau du stock, par des équations diﬀéren-tielles en utilisant la transformée de Laplace. Ensuite, Towill [Towill (1982)] a repris la même logique en adoptant une représentation par schéma-block. Les ordres de produc-tion délivrés sont fonction du déficit du niveau du stock et de la demande entrante. Ce modèle à été étendu, tout en considérant que le niveau du stock désiré est estimé à partir d’une fraction des prévisions de la demande [Edghill et Towill (1989), Sterman (1989)], ce qui aboutit à la variante Variable Inventory Order Based Production Control System connue sous l’acronyme VIOBPCS. Un peu plus tard, les travaux de [John et al. (1994)] ont montré la nécessité de prendre en compte l’encours de production à travers la chaîne, noté WIP 2, et qui a un eﬀet indéniable sur la variation du niveau de stock. Tout cela a donné naissance au modèle APIOBPCS, qui permet donc la prise en compte l’encours de production en plus de la demande et de la consigne du niveau de stock.

Spécifications des systèmes contraints

Comme précédemment cité, le système logistique est soumis à des contraintes struc-turelles, liées à la nature physique intrinsèque du système. Le modèle proposé doit alors prendre compte ces contraintes que nous formalisons de la façon suivante.
a) Contraintes de stockage. Dans un système logistique, la capacité de stockage est limitée par la taille et la contenance des espaces, alloués à la fonction de stockage des produits. De ce fait, le niveau du stock yptq ne peut dépasser une certaine valeur, que nous notons ymax, correspondant à cette capacité maximale de contenance. Aussi, un niveau de stock est une grandeur toujours positive, car il quantifie de la matière mesurée en nombre de pièces, de sorte qu’il est limité par un paramètre minimale de dimensionnement noté ymin. Ainsi, à tout instant t, yptq vérifie la contrainte suivante : 0 ⁄ ymin ⁄ yptq ⁄ ymax. (1.5)
b) Contraintes de production. De la même façon, les ordres de production sont aussi des grandeurs physiques positives, qui ont des limites sur les ressources de production. Celles-ci présentent des seuils de saturation qu’il est nécessaire de res-pecter, et qui présentent de vrais freins lors de la mise en pratique du modèle. En notant umin et umax les capacités minimale et maximale de production respecti-vement, les contraintes sur les ordres de production se présentent sous la forme suivante : 0 ⁄ umin ⁄ uptq ⁄ umax. (1.6)
c) Spécification de la demande. La contrainte que nous présentons sur le flux de demande, est une spécification de fonctionnement. Dans notre travail, nous considérons que la demande dptq est inconnue, de sorte que le modèle et les résultats que nous présentons par la suite, restent valables tant pour une demande constante, que pour une demande saisonnière ou aléatoire. Néanmoins, la demande est aussi une grandeur physique positive et limitée par deux valeurs, l’une étant minimale et l’autre maximale, que nous notons dmin et dmax respectivement. Cette spécification se formalise sous la forme suivante : 0 ⁄ dmin ⁄ dptq ⁄ dmax. (1.7)

Le rapport de stage ou le pfe est un document d’analyse, de synthèse et d’évaluation de votre apprentissage, c’est pour cela clepfe.com propose le téléchargement des modèles complet de projet de fin d’étude, rapport de stage, mémoire, pfe, thèse, pour connaître la méthodologie à avoir et savoir comment construire les parties d’un projet de fin d’étude.

Table des matières

Introduction générale
I Positionnement et problématique de la thèse
1 Contexte et méthodologie de recherche
1.1 Introduction
1.2 Sur les systèmes logistiques
1.3 Enjeux de la gestion des systèmes logistiques
1.3.1 Indicateurs de performance
1.3.2 Facteurs de variabilité et effet « Bullwhip »
1.4 Étude des systèmes logistiques
1.4.1 Modèles et outils de modélisation
1.4.2 Modèles analytiques des systèmes logistiques
1.4.3 Méthodes de gestion des stocks
1.5 Modèle du système logistique basique
1.5.1 Dynamique du stock dédiée aux produits périssables
1.5.2 Spécifications des systèmes contraints
1.6 Modèle général des réseaux logistiques
1.6.1 Équation fondamentale de la dynamique des stocks
1.6.2 Spécifications et contraintes de fonctionnement
1.7 Approche de commande des systèmes contraints
1.8 Conclusion du chapitre
2 Outils mathématiques de base
2.1 Introduction
2.2 Modélisation des systèmes à retards
2.3 Stabilité des systèmes à retards
2.3.1 Stabilité Entrée-Sortie
2.3.2 Stabilisation par prédiction d’état
2.4 Calcul des bornes pour un système Entrée-Sortie monovariable
2.5 Bornes du système Entrée-sortie multivariable
2.5.1 Polyèdres et ensembles convexes
2.5.2 Calcul des bornes pour un système multivariable
2.6 Principe d’invariance et invariance polyédrale
2.6.1 Conditions d’invariance du système monovariable
2.6.2 Propriétés d’invariance polyédrale
2.7 Méthode d’élimination de Fourier Motzkin
2.8 Approche structurelle
Conclusion et objectifs de la thèse
II Commande par invariance d’une classe de systèmes de convolution
3 Pilotage du système logistique en configuration réseau
3.1 Introduction
3.2 Description du modèle multivariable
3.3 Passage du modèle retardé au modèle réduit
3.4 Intervalle multivariable
3.5 Conditions de D-invariance contrôlée contrôlée du système réduit
3.5.1 Caractérisation du polytope invariant
3.5.2 Paramétrisation de la loi de commande
3.5.3 Complexité algorithmique de résolution
3.6 Conditions d’admissibilité du système à retards
3.7 Discussion de l’étude
3.8 Conclusion du chapitre
4 Application des résultats sur une chaîne logistique 98
4.1 Introduction
4.2 Système d’étude
4.3 Du système réduit au système découplé
4.4 Construction des polytopes
4.5 Structure de commande admissible
Conclusion partielle
III Pilotage du système logistique élémentaire
5 Solution de pilotage par principe d’invariance
5.1 Introduction
5.2 Stratégie de commande
5.2.1 Solution par prédiction d’état
5.2.2 Loi de commande de type bang-bang
5.3 Conditions de D-invariance
5.4 Conditions d’admissibilité de la loi de commande
5.4.1 Conditions nécessaires et suffisantes pour le régime établi
5.4.2 Phase d’initialisation
5.5 Exemple de simulation
5.6 Optimisation de la loi de commande
5.7 Conclusion du chapitre
6 Solution de pilotage des flux par une commande linéaire
6.1 Introduction
6.2 Structure de la loi de commande linéaire
6.3 Dynamique des flux d’entrée et de sortie
6.4 Les bornes atteignables par les variables des flux
6.5 Ensemble de conditions initiales admissibles
6.6 Mise en œuvre de la loi de commande
6.6.1 Conditions admissibles de la loi de commande
6.6.2 Paramètres de la loi de commande
6.7 Comparaison des lois de commande Bang-Bang et linéaire
6.8 Exemple de simulation
Conclusion partielle
IV Étude de robustesse de la commande linéaire vis-à-vis d’incertitudes
7 Stabilité de la commande linéaire
7.1 Introduction
7.2 Structure de commande
7.3 Transfert en boucle fermée
7.4 Conditions de stabilité robuste
7.5 Choix des paramètres de commande
7.6 Impact des incertitudes sur le dimensionnement du système logistique
7.7 Conclusion du chapitre
8 Robustesse vis-à-vis d’incertitudes sur le retard
8.1 Introduction
8.2 Structure de prédiction : problème et solution
8.3 Dynamique de la prédiction du stock
8.4 Bornes atteignables des variables entrée-sortie
8.5 Conditions d’admissibilité de la loi de commande
8.6 Étude de cas pour un retard exact
8.7 Exemple de simulation
8.8 Conclusion du chapitre
9 Robustesse vis-à-vis d’incertitude sur le facteur de perte
9.1 Introduction
9.2 Stratégie de commande
9.3 Propriétés de la structure de prédiction
9.4 Bornes atteignables des flux entrée-sortie
9.5 Loi de commande admissible
9.6 Exemple de simulation
9.7 Conclusion du chapitre
Conclusion générale
Annexe
Bibliographie